Narayan Chandra Pradhan*

Empirical verification of export-led growth (ELG) hypothesis by applying various time series techniques reveals both short- and long-run relationship between export growth and output growth. The research question that has been addressed in the study is: whether openness has impact on growth, and if so, then in what direction? Bivariate Granger causality test suggests that the direction of causality runs from export growth to GDP growth. This fact implies that one can use exports to better predict the GDP than simply by the past history of GDP. The aim is to substantiate the importance of exports in the growth process of Indian economy after its opening up to the world economy.

JEL Classification : F1, F43, O53.
Keywords : International Trade in Goods and Services, Economic Growth, India

I. Introduction

Economists across the board have agreed with the opinion that the process of economic growth is an extremely complex phenomenon. It depends on many variables, such as, capital accumulation (both physical and human), international trade, price condition, political situation, income distribution, and even more on geographical factors. Export-led growth (ELG) hypothesis postulates that export expansion is one of the prime determinants of economic growth. The overall growth of countries can be generated not only by increasing the amounts of labour and capital within the economy as the classical economists postulates, but also by expanding exports to wider markets. According to the proponents of ELG hypothesis, exports can perform the function of an ‘engine of growth’. The association between exports and economic growth is often attributed to the positive externalities for the domestic economy arising from participation in world markets, for instance, from the re-allocation of existing resources, economies of scale and various labour-specialisation effects (Bhagwati, 1978; Krueger, 1978).

The term ELG hypothesis is seldom explicitly defined in economic literature. However, it is clear that most authors have in mind some notion of a multiplier effect, whereby, an initial favourable shock in the export sector sets in motion forces leading to additional economic growth. Kindleberger (1962) defines trade as a leading sector when ‘exports rise would lead to an incentive for the establishment and expansion of other peripheral activities’. Meier (1976) explained that the export sector acts ‘as a key propulsive sector, propelling the rest of the economy forward’. In keeping with the spirit of these definitions, the criterion adopted here for ‘strong export-led growth’ (SELG) is that expansion in the export sector should stimulate aggregate capital accumulation. This is the natural criterion in that with a larger capital stock the increase in steady-state growth is greater than the direct gain conferred by the terms of trade improvement or resource discovery. An increase in the steady-state capital stock is a necessary but not sufficient condition for growth to be higher in the long run. If it can be established that steady-state growth increases despite a decline in the aggregate capital stock, the outcome will be labelled as ‘weak export-led growth’ (WELG). Finally, when capital decumulation is severe enough to lower steadystate growth, the outcome will be characterised as ‘export-led fizzle’ (ELF).

In fact, during the 1990s a new series of empirical studies has been conducted on a number of divergent lines of research methodologies, time periods and countries. A key aspect of the earlier studies is related to both the analytical and the econometrics technique used. Earlier studies could have been misleading in the sense that they advocated export expansion in an indiscriminate way (Feder, 1982). In fact, the evidence available is inconclusive and this situation explains to some extent why this debate still exists in the economic literature. Added to this debate is the question of whether strong economic performance is ‘export-led’ or ‘growth-driven’. This question is important because the determination of the causal pattern between export and economic growth has important implications for policy-makers’ decision about the appropriate growth and development strategies.

Although, most studies focus on the causal link between exports and output growth in industrialised countries (Marin, 1992; Serletis, 1992; Henriques and Sadorsky, 1996), some researchers have examined the export-led growth hypothesis with emphasis on developing countries (Michaely, 1977; Balassa, 1978). Using data from selected industrialised countries, Marin (1992) examines the causal link between exports and productivity and finds that the exportled growth (ELG) hypothesis cannot be rejected for Germany, Japan, the United Kingdom, and the United States. Henriques and Sadorsky (1996) similarly focused on the export and output growth relationship for Canada using three variables (GDP, exports, and terms of trade). They employ a multivariate cointegration estimation methodology that accounted for potential feedback and simultaneity effects between these three variables. In contrast to Serletis’s (1992) earlier result, Henriques and Sadorsky (1996) find that ‘changes in GDP precede
changes in exports’.

The lack of consistent causal pattern between exports and output growth in earlier studies may be due to one or more of the following issues. The causal models in those studies may be mis-specified because of: (i) the omission of an important variable, such as, capital and foreign output growth; (ii) the traditional Granger causality F-test in a regression context may not be valid if the variables in the system are cointegrated, since the test statistic does not have a standard distribution (Toda and Philips, 1993); and (iii) temporal aggregation issues from the use of annual time series may yield erroneous causation results (Bahmani-Oskooee and Alse, 1993).

Consequently, the purpose of this article is to examine the nexus between export growth and economic growth and test the ELG
hypothesis for Indian economy. The analysis has three distinctive features differentiated from earlier empirical studies: (i) the study has gone beyond the traditional neo-classical theory of production function by estimating an augmented Cobb-Douglas functional form, which includes exports using annual data for the period 1970-71 to 2009-10. This study also includes services exports to that of merchandise one, as earlier studies generally based upon; (ii) the analysis carried out by focussing on a single country – India, instead of cross-country comparison; (iii) the study has examined empirically the long-run relationship, using procedures like unit root tests, stationarity, cointegration, Granger causality and vector autoregresion (VAR). Thus, the aim is to substantiate the importance of exports in the ‘growth process of Indian economy’ after its opening up to the world economy.

II. Literature Survey

II.1 Literature on ELG Hypothesis

For the last two decades, there has been massive resumption of economic growth literature triggered by the ‘endogenous growth
theory’, which has led to the propagation of models that stress the importance of trade in achieving a sustainable rate of economic growth. These models have focused on different variables, such as, degree of openness, real exchange rate, tariffs, terms of trade and export performance, to verify the hypothesis that open economies grow more rapidly than the closed ones (Edwards, 1998). Although, most models emphasised the nexus between trade and growth, they stressed that trade is only one of the variables that enter the growth equation. However, the advocates of the ELG hypothesis have stated that trade, in fact, was the main engine of growth in Southeast Asia. They argue that, for instance, Hong Kong, Taiwan, Singapore and South Korea, the so-called Four Tigers, have been successful in achieving high and sustained rates of economic growth since the early 1960s because of their free-market and the outward-oriented economies (World Bank, 1993). The literature concerning the relationship between trade and growth is also the consequence of the many changes that have taken place in the fi elds of development economics and international trade policy.

Although, a substantial part of the earlier studies found evidence of a correlation between exports and growth which was used to support the ELG hypothesis, this tends to hold only for cross-sectional studies. In fact, the recent evidence on time series, which makes extensive use of cointegration techniques, casts doubts on the positive effects of exports on growth in the long-run, and is thus not as conclusive as it was previously thought.

Among earlier major empirical studies, Emery (1967), Syron and Walsh (1968), Heller and Porter (1978), Bhagwati (1978) and Krueger (1978) can be mentioned. These studies explained economic growth in terms of export expansion alone in a two-variable framework. That is, they used bi-variate correlation - the Spearman’s rank correlation test - in cross-country format to illustrate the superior effects of the ELG hypothesis (Lussier, 1993). A second group of researchers, which includes Balassa (1978), Tyler (1981), Feder (1982), Kavoussi (1984), Ram (1985, 1987) and Moschos (1989) studied the relationship between export and output performance within a neo-classical framework. In most of these studies exports were included in an ad hoc manner in the production function, together with labour and capital. They claimed that by including exports they were taking into consideration a broad measure of externalities and productivity gains generated by this sector which stimulated the domestic economy. The majority of these investigations aimed at analysing developing countries by using ordinary least squares (OLS) on cross-section data and used their results to demonstrate the advantages of the export promotion strategy in comparison with the import substitution policy.

For most of the country-specific studies, both industrialised and developing, the empirical investigations found no long-run relationship between exports and economic growth; rather, the studies suggest that it arises only from a positive short-term relationship between export expansion and growth of gross domestic product (GDP). The studies of industrialised nations have analysed the cases of Canada, France, Germany, the United Kingdom, the United States and Switzerland, among others. In only a few cases have the empirical results confirmed that export expansion was a key element in the economic success of those countries (Kugler, 1991; Afxentiou and Serletis, 1991; Henriques and Sadorsky, 1996). Even more surprising is the finding in relation to Japan, which states that internal forces were the handmaidens of the great Japanese economic success in the twentieth century, including the post-war period, and not trade as many have claimed in the recent past (Boltho, 1996).

The most recent time series investigations concerning developing countries that have used the econometric methodology of cointegration have not been able to establish unequivocally that a robust relationship between these variables indeed exists in the long term, namely that the variables are cointegrated (Islam, 1998). While some have been able to find a long-run relationship, many others have rejected the ELG hypothesis i.e., that export expansion causes growth in the long run. In fact, in most studies the results suggest that this arises owing to a simple short-term relationship, a feature that is not surprising, if we take into account the fact that the studies that have concentrated their attention on industrialised nations have also been unable to find a robust relationship between these variables (Kugler, 1991).

Berg and Schmidt (1994) found cointegration in 11 of the 16 Latin American Countries analysed. In fact, in the case of Costa Rica they were able to verify the existence of a long-term relationship. Although the result seems to endorse in general the export-led hypothesis, they seem to deviate from those recently reported by the empirical literature (Rodrik, 1999). However, a possible justifi cation of the positive results obtained in the investigation conducted by Berg and Schmidt (1994) is that these researchers employed population and investment as proxies for the appropriate aggregate inputs, i.e. labour force and capital stock. Although they have been widely used in many cross-section growth studies as well as time series analysis (Al-Yousif, 1997), many researchers have had serious doubts about them and have thus expressed their suspicion regarding studies that have tested the export promotion hypothesis by using, for instance, the investment-output ratio, i.e. gross domestic investment (GDI)/gross domestic product (GDP), as opposed to capital stock or population instead of labour force.

Though, there are numerous facets to the trade-growth nexus, most of the literature has concentrated on disturbances connected with the export sector. The ELG hypothesis has frequently been invoked to explain differences in development patterns among developing countries. The trade theorists have also examined the growing concern over the potentially adverse effects of a booming natural resource based export sector termed as Dutch Disease phenomenon. The literature on this special aspect focus on the impact of a rise in export revenues from an inelastically supplied, resource intensive product that uses little capital or labour and is not consumed domestically - and tends to make de-industrialisation, not aggregate growth, its principal concern (Buffie, 1992).

Despite the sizeable literature generated by the ELG hypothesis, little is known about how various export shocks might affect the
economic growth. The numerous case studies done by development economists and economic historians are full of suggestive ideas but do not point to any firm conclusions. Country experiences have varied widely and in the absence of any explicit theoretical framework linking export shocks and the main determinants of economic growth. It is, thus, difficult to judge whether export sector expansion has stimulated growth, retarded growth, or merely accompanied growth or contraction in the rest of the economy (Kindleberger, 1961; Kravis, 1970; Meier, 1976).

There have been studies on the existence of a threshold effect as well (Kavoussi, 1984; Moschos, 1989). These studies have been supplemented by causality tests (Jung and Marshall, 1985). The econometric methods employed in these analyses have been significantly influenced by the work of Granger (1969), Engle and Granger (1987), and Johansen and Juselius (1990), among others. The studies such as Jung and Marshall (1985), Afxentiou and Serletis (1991), and Dodaro (1993) have cast some doubt on the validity of the ELG hypothesis. Others such as Serletis (1992), Henrique and Sadorsky (1996), Bahmani-Oskooee and Alse (1993), and Nidugala (2001) provide fairly robust evidence in favour of the ELG hypothesis. Most of the time series studies employ the Granger method, while only a few studies combine Granger’s test with the Akaike’s Information Criterion (AIC) to determine the optimal lag length in the Granger causality test. The latter approach removes the ambiguity involved in the arbitrary choice of lag lengths.

The idea that export growth is one of the major determinants of output growth - ELG hypothesis - is a recurrent one. Export growth may affect output growth through positive externalities on nonexports, through the creation of more efficient management styles, improved production techniques, increased scale economies, improved allocative efficiency, and better ability to generate dynamic comparative advantage. If there are incentives to increase investment and improve technology, this would imply a productivity differential in favour of the export sector. It is thus argued that an expansion of exports, even at the cost of other sectors, will have a net positive effect on the rest of the economy (Balassa, 1978). It may also ease the foreign exchange constraint. There could also be positive spillover effects on the rest of the economy. These factors, notwithstanding, the empirical evidence for the ELG hypothesis is mixed.

II.2 ELG Hypothesis: Studies on India

There is fair amount of literature on ELG hypothesis pertaining to Indian economy. Majority of the empirical studies found lack of
causality between export and economic growth in both directions. Jung and Marshall (1985) and Dodaro (1993) reported an insignificant F-statistic for real export growth to real income growth as well as in other way round, although the sign is positive in both cases. Similarly, Dhawan and Biswal (1999) investigate the ELG hypothesis using a vector autoregressive (VAR) model by considering the relationship between real GDP, real exports and terms of trade during 1961-1993. They employ a multivariate framework using Johansen’s cointegration procedure and find a long-run equilibrium relationship between these three variables and the causal relationship flows from the growth in GDP and terms of trade to the growth in exports. However, they conclude that the causality from exports to GDP appears to be a short-run phenomenon. In a similar framework, Asafu-Adjaye et al. (1999) consider three variables: exports, real output and imports for the period 1960-1994. They do not find any evidence of the existence of a causal relationship between these variables in case of India and no support for the ELG hypothesis, which is not too surprising given India’s economic history and trade policies. Anwer and Sampath (2001) also find evidence against the ELG hypothesis for India.

Mallick (1996), using annual data for the period 1950-92 and employing Engle-Granger cointegration cum error-correction procedure, finds a strong cointegration between income and exports, and that the direction of causality runs from income growth to export growth (i.e., growth-led exports). While the Granger-causality tests, in his study, are sensitive to the lag length chosen and do not show consistent causal flow from income growth to export growth, the results of the error-correction model show that causation runs from income growth to export growth (as the error-correction term is significant) irrespective of the lag length chosen. This seems to suggest that the causality found by Mallick (1996) is a long-term phenomenon.

Nidugala (2001) finds evidence in support of the ELG hypothesis, particularly in the 1980s. His study reveals that growth of manufactured exports had a significant positive relationship with GDP growth, while the growth of primary exports had no such infl uence. Ghatak and Price (1997) test the ELG hypothesis for India during 1960-1992, using ‘GDP net of exports’ as regressor, along with exports and imports as additional variables. Their results indicate that real export growth Granger-caused by non-export real GDP growth over the period 1960-1992. Their cointegration tests confirmthe long-run nature of this relationship. However, imports do not appear to be important in those studies.

Chandra (2002), on the other hand, finds that export growth and GDP growth are interlocked in a two-way relationship as opposed to Mallick (1996). Chandra also finds that real exports and real GDP are not cointegrated in lndia, implying that there is no long-run relationship between them. Sinha (1996) envisaged the relationship between openness and economic growth in India,
wherein, two types of analysis were performed. First, long run relationship between GDP and openness was studied. Secondly, tests were performed to find the causal relationship between GDP and openness. The result of the Granger causality test shows that there is a two-way causality between the growth of GDP and openness. Thus, a reduction in trade barriers is likely to promote economic growth i.e., the results of the study show that openness contribute to growth of GDP which implies that both exports and imports contribute to economic growth in the long run.

Marjit and Raychaudhari (1997) have analysed the implications of specific trade policies on exports and gross domestic products. They assumed that all the domestic demand will be catered by domestic production which leads to a decline in exports to some extent. In case of India, GDP granger causes export growth (yearly data for 1951 to 1994), but not vice versa according to their results. The volume of imports was hypothesised to be an increasing function of the real GDP and foreign exchange reserves and decreasing function of the relative price notion. A dummy variable was also introduced to account for the introduction of economic reforms. The study found that a growth in exports volume was due to growth in real income. The ordinary least square results of the study indicate that income elasticity of exports (with respect to world real income) is higher than the income elasticity of imports.

Sharma and Panagiotidis (2004) re-examines the sources of growth for the period 1971-2001 based upon Feder’s (1982) model to
investigate empirical relationship between export growth and GDP growth (the export led growth hypothesis). They investigate the
following hypotheses: (i) whether exports, imports and GDP are cointegrated using the Johansen approach and Breitung’s nonparametric cointegration test, (ii) whether export growth Granger causes GDP growth, and (iii) whether export growth Granger causes investment. They fail to find support for the hypothesis that exports Granger cause GDP, using two measures for GDP (GDP with exports and GDP without exports). The same also holds for the relationship between exports and investment.

From the review of empirical literature on exports and growth, it is clear that the exports do not necessarily cause growth. The results reported are clearly sensitive to the variables employed, theoretical approach used and even on the econometric methodology employed. For example, cross-section studies are more likely to corroborate a positive relationship between exports and growth, while the results of time series studies depend substantially on the countries analysed, the period chosen and the econometric methods used. In addition, since cross-section studies can obscure particularities of developing countries, especially, those that are low-income countries, the correct strategy to follow from an empirical point of view is to address the issue in a single country framework, using as much as possible the recent developments in time series analysis.

III. Empirical Analysis and Results

III.1 Data, Source and Explanations

The data set consists of observation on India’s export of goods and services, real GDP, gross domestic capital formation, real effective exchange rate, and the world GDP. It may be mentioned that, there are two basic sources for data on India’s exports. One set is compiled by the Directorate General of Commercial Intelligence and Statistics (DGCI&S), Ministry of Commerce and Industry, Government of India and the other set is compiled by the Reserve Bank of India (RBI). The DGCI&S compiles information on real transactions, reporting quantities/volumes of exports as well as export earnings in Rupee terms. Merchandise exports are decomposed into headings compatible with the ITC (HS)¹ Standard Industrial Classification (SIC) codes. Thus, merchandise exports are disaggregated by SIC categories and by destination (i.e. according to commodity and country Classification). The RBI export data (both goods and services) is compiled by aggregating the economy-wide financial transactions related to exports, as reported by exporting firms. Exporters and financial intermediaries have to provide this information to RBI on the basis of statutory provision. DGCI&S data has been used frequently in the trade analysis as the case of merchandise data is concerned. RBI’s data based on Balance of Payments (BoP) basis has been used relatively less frequently. As the current study is concerned with services exports as well, it is decided to use the RBI’s data sets for our analysis. Accordingly, the data used in this exercise has been obtained from the ‘Handbook of Statistics on the Indian Economy 2009-10’ (HBSIE). The data for the current empirical analysis pertaining to the period 1970-71 to 2009-10 compiled from HBSIE, partly owing to ease of availability at this end, and partly for using exports of both goods and services.

The time series data on real GDP and gross domestic capital formation (GDCF) are obtained from the ‘Central Statistical Organisation’ of the Government of India (Base Year: 1999-2000), the same is also published in HBSIE for the period 1970-71 to 2009-10. The time series data on real effective exchange rate (REER) are calculated from the RBI’s HBSIE based on splicing methodology. It may be mentioned that the data on REER up to 1992 are based on official exchange rates and data from 1993 onwards are based on Foreign Exchange Dealers’ Association of India (FEDAI) indicative rates. REER indices are recalculated from April 1993 onwards using the new wholesale price index (Base: 1993-94=100). A new 6-currency REER series (Trade-based weights) has been introduced with effect from December 2005.

The data set is annual and covers the period 1970-71 (financial year data represented by 1970 in econometric analysis) to 2009-10 (similarly represented by 2009). The data description and their specifications in empirical analysis are as follows:

(1) RGDP: Real GDP (GDP at factor cost at constant prices; Base: 1999-2000).

(2) EXGD: Exports of Goods (Merchandise exports on BoP basis)

(3) EXGS: Exports of Goods and Services (clubbing of Merchandise exports and Non-factor services receipts, both on BoP basis).

(4) GDCF: Gross Domestic Capital Formation at constant prices (Base: 1999-2000).

(5) REER: Real Effective Exchange Rate (Index).

(6) WGDP: World GDP (in value).

All the above series are subjected to logarithmic transformations. The prefix ‘L’ stands for the natural logarithm of the respective time series, ‘R’ stands for the residuals of the respective regression, and ‘D’ denotes differencing of the respective time series. It is appropriate to mention that, all econometric exercises are carried out by using EViews.

III.2 Tests of Unit Root and Stationarity

Before proceeding to the test the ELG hypothesis, it is appropriate that all the series be tested for stationarity or the ‘same statistical property’ - means the series have to be differenced or de-trended by the same number of times to render them stationary. The traditional approach of first differencing disregards potentially important equilibrium relationships among the levels of the series to which the hypotheses of economic theory usually apply (Engle and Granger, 1987).

The early and pioneering work on testing for a unit root in time series was done by Dickey and Fuller (Fuller, 1976; Dickey and Fuller, 1979). The basic objective of the test is to examine the null hypothesis

The null hypothesis of a unit root is rejected in favour of the stationary alternative in each case if the test statistics is more negative than the critical value. Accordingly, Time series univariate properties were examined using two unit root tests: augmented Dickey and Fuller (1979) and Phillip and Perron (1988) tests. The PP tests are similar to ADF tests, but they incorporate an automatic correction to the DF procedure to allow for autocorrelated residuals. The tests often give the same conclusions as, and suffer from most of the same important limitations as, the ADF tests.

Table 1 summarises the results for unit root tests on levels and in first differences (at ‘maximum lags 2’ with ‘trend and intercept’
included in the test equation) of the data. For the ADF tests, the lag length is based on the Akaike Information Criterion (AIC), while for the PP test bandwidth selection is based on Newey-West. It is evidenced from the test statistics that all the time series are I(1). Under the classical hypothesis testing framework, the null hypothesis is never accepted, it is simply stated that it is either ‘rejected’ or ‘not rejected’. This means that a failure to reject the null hypothesis could occur either because the null was correct, or because there is insufficient information in the sample to enable rejection (Brooks, 2008).

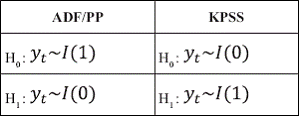
The most important criticism that has been levelled at unit root tests is that their power is low if the process is stationary but with a root close to the non-stationary boundary. Stationarity tests have stationarity under the null hypothesis, thus reversing the null and alternatives under the Dickey-Fuller approach. Thus under stationary tests, the data will appear stationary by default if there is little information in the sample. One such stationarity test proposed by Kwaitkowski, Phillips, Schmidt, and Shin (1992), in short, the KPSS test on the levels series presented in Table 2. We have now observed that the test statistics exceeds the critical value even at 1% level, so that the null hypothesis of a stationary series is strongly rejected. The results of these tests can be compared with the ADF/PP procedure to see if the same conclusion is obtained. The joint use of unit root tests and stationarity is known as confirmatory data analysis. The null and alternative hypotheses under each testing approach are as follows:

For the conclusion to be robust, the results should fall under outcomes (1) or (2) above.

By conducting tests under both types of the null hypotheses, the results are much more robust than if just one of the tests is used, provided of course that the results of the two tests are compatible. In all cases, both the tests confirm the same conclusion – all the variables under examination are having property I(1). The results of the unit root tests performed corroborate previous findings in the empirical literature, i.e. as with most macroeconomic series, the variables under consideration in this study appear to be non-stationary and trended in levels. Only their first differences are stationary.

Consequently, the next section of the empirical study investigates whether the series under scrutiny are cointegrated, so that a welldefi ned linear relationship exists among them in the long run. Thus, we proceed to test for cointegration between the variables on levels using several tests, all of which are based on the ‘null hypothesis of no cointegration’.

III.3 Tests of Cointegration (Engle-Granger Approach)

In most cases, if two variables that are I(1) are linearly combined, then the combination will also be I(1). Most generally, if variables with differing orders of integration are combined, the combination will have an order of integration equal to the largest. This linear combination of I(1) variables will itself be I(1), but it would obviously be desirable to obtain residuals that are I(0), so that the variables are cointegrated.

According to Engle and Granger (1987), a set of variables is defined as cointegrated, if a linear combination of them is stationary. Many time series are non-stationary but ‘move together’ over time – that is, there exist some influences on the series (for example, market forces), which imply that the two series are bound by some relationship in the long run. A cointegrating relationship may also be seen as a long term or equilibrium phenomenon, since it is possible that cointegrating variables may deviate from their relationship in the short run, but their association would return in the long run. An interesting question is: whether a potentially cointegrating regression should be estimated using the levels of the variables or the logarithms of the levels of the variables. Hendry and Juselius (2000) noted that, if a set of series is cointegrated in levels, they will also be cointegrated in log levels. It is common to run a regression of the log of the series rather than on the levels; the main reason for using logarithms is that differences of the logs are growth rates, whereas this is not true for the levels.

In the main case under scrutiny (Screenshots 1A and 1B): the ELG hypothesis represented by cointegration sub-tests are able to find evidence in favour of long run relationship between real GDP and exports independently of other variables in case of the Indian economy. When variables are cointegrated, the OLS estimates from the cointegrating regression will be super consistent, implying that the estimates approach their true parameters at a faster rate than if the variables were stationary and not cointegrated (Gujarati, 2003). The presence of a cointegrating relationship forms the basis of error correction specification. One can treat error term as equilibrium error.

III.4 Equilibrium Correction or Error Correction Model

The error correction mechanism (ECM) was first used by Sargan (1984) and later popularised by Engle and Granger (1987). An important theorem known as Granger Representation Theorem states that if two variables Y and X are cointegrated, then the relationship between the two can be expressed as ECM. The error correction model takes the following form of equation:

In both cases (Screenshots 2A and 2B), the coefficients of the error correction term have the desired sign (negative). About 17 per cent of disequilibrium is corrected every year in case of cointegration between ‘exports of goods’ and GDP and about 14 per cent disequilibrium corrected every year in case of ‘exports of goods and services’ and GDP. The significance of the error correction term at 5% level confirms that exports and GDP are cointegrated in the long run and error correction takes place in the short run.

One of the major drawbacks of Engle-Granger approach is that it can estimate only up to one cointegrating relationship between the variables. But in other situations, if there are more variables, there could potentially be more than one linearly independent cointegrating relationship. Thus it is appropriate to examine the issue of cointegration within the Johansen’s VAR framework.

III.5 Johansen Cointegrating Systems based on VAR

The Johansen procedure is a multiple equation method that permits the identification of the cointegration space, which enables the testing of how many cointegration relationships exist. LRGDP, LEXGS, LGDCF, LREER and LWGDP are tested under Johansen’s technique and results displayed in Screenshots 3A and 3B.

The trace test in Screenshot 3B indicates that the test statistics of 124.02 considerably exceeds the critical value 69.82 and so the null of no cointegrating vectors is rejected. This continues, until we do not reject the null hypothesis of at most 2 cointegrating vectors at the 5% level. The max test also confirms this result.

Suppose, we want to test the hypothesis that the LREER and LWGDP do not appear in the cointegrating equation. We could test this by specifying the restriction that their parameters are zero. In this case there are two restrictions, so that the test statistics follows a Chi-square distribution with 2 degrees of freedom. The p-value for the test is 0.0004, so the restrictions are not supported by the data and we could conclude that the cointegrating relationship must also include the LREER and LWGDP (Screenshots 4A and 4B).

The result thus demonstrate that the considered variables are cointegrated in that there is a long-run equilibrium relationship among them (these series cannot move too far away from each other or they cannot move independently of each other). The fact that the variables are cointegrated implies that there is some adjustment process in the short run, preventing the errors in the long run relationship from becoming larger and larger.

III.6 Granger Causality Test: Empirical Finding

The Null Hypothesis (Ho) in each case is: the variable under consideration does not Granger cause the other variable.

The result in Tables 3A and 3B suggests that the direction of causality is from export growth to GDP growth; since the estimatedF-statistics is significant, at the 5% level up to 4 lags, at the 10% level at lag 5. On the other hand, there is no “reverse causation” from GDP growth to export growth, since the F-statistics is statistically insignificant. It can be assessed that, at lag 6, there is no statistically discernible relationship between the two variables. This reinforces the point made earlier that the outcome of the Granger causality test is sensitive to the number of lags introduced in the model. In the next Table, we have presented the Granger causality between GDP and Exports of Goods and services. This indicates that one can use exports to better predict the GDP than simply by the past history of GDP.

III.7 Block Exogeneity/Granger Causality in VAR: Empirical Estimates

The first step in the construction of any VAR model, once the variables that will enter the VAR have been decided, will be to determine the appropriate lag length. This can be achieved in a variety of ways, but one of the easiest is to employ a multivariate information criterion (Screenshot 5). EViews presents the values of various information criteria and other methods for determining the lag order. In this case, the Schwartz criteria select a zero order as optimal, while Akaike’s and Hannan-Quinn criterion chooses VAR(5).

Following the lag order selection criteria, I have tested Granger causality/Block Exogeneity in VAR framework. The result indicates lead-lag relationship between exports and GDP and Granger causality is significant at 5% level from exports of Goods and Services to GDP; ‘significant at 10% from exports to GDCF’ but no causality in the opposite direction (Screenshot 6). The result can be interpreted as movements in the exports of goods and services appear to lead that of GDP in case of Indian economy.

IV. Concluding Observations

Application of stationarity/unit root tests, viz., ADF, PP and KPSS, confirms that all the variables are non-stationary at log levels
and there is existence of unit root in the series used in the study. In other words, all the macroeconomic variables used in this study are I(1) in log levels and become stationary after first differencing their log levels. Subsequent residual-based cointegration test on log levels between exports and GDP confirms their long run relationship. This result sets the stage for application of error correction model in bivariate as well as multivariate frameworks. The bivariate error correction model indicates that, in short run, if the GDP is above its equilibrium value, it will start falling in the next period to correct the equilibrium error. The coefficient of error correction term decides how quickly the equilibrium is restored. About 17 per cent of disequilibrium is corrected every year in case of exports of goods and GDP; and about 14 per cent disequilibrium is corrected every year in case of ‘goods and services’ and GDP. The significance of the error correction term at 5% level suggesting the robust relationship between export growth and growth of real GDP. This reinforces the nexus between export and GDP growth in both short and long run.

The test of cointegrating relationship among a set of chosen variables in Johansen’s procedure: the trace test indicates the null of
no cointegrating vectors is rejected. This continues, until we do not reject the null hypothesis of at most 2 cointegrating vectors at the 5% level. The max test also confirms this result. In the subsequent specification of restriction under Vector Error Correction Model (VECM) in VAR, we dropped LREER and LWGDP to test the hypothesis that these two variables do not appear in the cointegrating equation. The p-value for the test is 0.0004 indicates that the restrictions are not supported by the data and we could conclude that the cointegrating relationship must also include the LREER and LWGDP. The result thus demonstrate that the considered variables are cointegrated in that there is a long-run equilibrium relationship among them (these series cannot move too far away from each other or they cannot move independently of each other). The fact that the variables are cointegrated implies that there is some adjustment process in the short run, preventing the errors in the long run relationship from becoming larger and larger.

The test of Granger causality suggests that the direction of causality from export growth to GDP growth; since the estimated F-statistics is significant, at the 5% level up to 4 lags, at the 10% level at lag 5. On the other hand, there is no “reverse causation” from GDP growth to export growth, since the F-statistics is statistically insignificant. It can be assessed that, at lag 6, there is no statistically discernible relationship between the two variables. This indicates that one can use exports to better predict the GDP than simply by the past history of GDP. Granger causality/Block Exogeneity in VAR framework indicates lead-lag relationship between exports and GDP and the result can be interpreted as movements in the exports of goods and services appear to lead that of GDP in case of Indian economy.

The conclusion supporting the validity of the ELG hypothesis is similar to results of Serletis (1992) in case of Canada and for other industrial countries as in Marin (1992). However, the caveat is that, import side of openness has not taken into consideration. Given the recent success of software exports from India along with the focus area approach to both merchandise and services exports including its diversification, the finding is plausible and consistent with prior expectation that increasing exports stimulate economic growth.

^* Research Officer, Department of Economic and Policy Research, Reserve Bank of India, Central Office, Mumbai. The author would like to thank Prof. Pushpa Trivedi and an anonymous referee for their insightful comments that helped further improvement. The views expressed in the article are author’s own. However, the usual disclaimer applies.

¹ International Trade Classification (Harmonised System) is an extended version of the International Classification system called ‘Harmonised Commodity Description and Coding System’ evolved by World Custom Organisation previously known as Customs Cooperation Council.

Dodaro, S. (1993), ‘Comparative Advantage, Trade and Growth: Export- Led Growth Revisited’, World Development, 19(9): 1153-65.

Edwards, S. (1998), ‘Openness, Productivity and Growth: What do we Really Know?’, The Economic Journal, 108: 383–98.

Emery, R. F. (1967), ‘The relation of exports and economic growth’, Kyklos, 20(2): 470-86.

Engle, R. F., and C. W. J. Granger (1987), ‘Cointegration and Error Correction: Representation, Estimation and Testing’, Econometrica, 55: 251-76.

Feder, G. (1982), ‘On Exports and Economic Growth’, Journal of Development Economics, 5: 59-73.

Fuller, W. A. (1976), Introduction to Statistical Time Series, John Wiley & Sons, New York.

Ghatak, S., and S. W. Price (1997), ‘Export Composition and Economic Growth: Cointegration and Causality Evidence for India’, Weltwirtschaftliches Archiv, 133(3): 538-53.

Granger, C. W. J. (1969), ‘Investigating Causal Relations by Econometric Models and Cross-Spectral Methods’, Econometrica, 37: 424-38.

Gujarati, D. N. (2003), Basic Econometrics, Fourth Edition, McGraw-Hill, New York.

Heller, P. S., and R. C. Porter (1978), ‘Exports and growth: An Empirical Re-investigation’, Journal of Development Economics, 5(2): 191-93.

Hendry, D. F. and K. Juselius (2000), ‘Explaining Cointegration Analysis: Part I’, Energy Journal, 21: 1-42.

Henriques, I., and P. Sadorsky (1996), ‘Export-led Growth or Growth-driven Exports: The Canadian case’, Canadian Journal of Economics, 29(3): 541-55.

Islam, M. N. (1998), ‘Exports expansion and Economic growth: Testing for Cointegration and Causality’, Applied Economics, 30(3): 415-25.

Johansen, S., and K. Juselius (1990), ‘Maximum likelihood and inference on Cointegration: with applications to the Demand for Money’, Oxford Bulletin of Economics and Statistics, 52: 169-210.

Jung, W. S., and P. J. Marshall (1985), ‘Exports, Growth and Causality in Developing Countries’, Journal of Development Economics, 18: 1-12.

Kavoussi, R. M. (1984), ‘Export expansion and Economic growth: Further empirical evidence’, Journal of Development Economics, 14: 241-50.

Kindleberger, C. P. (1962), Foreign Trade and the National Economy, Yale University Press, New Haven, CT.

Kravis, I. B. (1970), ‘Trade as a Handmaiden of Growth: Similarities between the nineteenth and twentieth centuries’, Economic Journal, 80: 850-72.

Krueger, A. O. (1978), Foreign Trade Regimes and Economic Development: Liberalisation Attempts and Consequences, Ballinger Pub. Co., Cambridge, MA.

Kugler, P. (1991), ‘Growth, exports and cointegration: An empirical investigation’, Weltwirtschaffliches Archiv, 127(1): 73-82.

Kwaitkowski, D., P. C. B. Phillips, P. Schmidt, and Y. Shin (1992), ‘Testing the Null Hypothesis of Stationarity against the alternative of a Unit Root’, Journal of Econometrics, 54: 159-78.

Lussier, M. (1993), ‘Impacts of exports on economic performance: A comparative study’, Journal of African Economics, 2(1): 106-27.

Mallick, S. K. (1996), Causality between exports and economic growth in India: Evidence from Cointegration based Error-Correction Model, Indian Journal of Economics, 76 (302), 307-320.

Marin, D. (1992), ‘Is the export-led growth hypothesis valid for industrialized countries?’, Review of Economics and Statistics 74, 678-88.

Marjit, S., and A. Raychaudhuri (1997), India’s Exports - An Analytical Study, Oxford University Press, New Delhi.

Meier, Gerald M. (1976), ‘Conditions of export-led development – A Note’, in Leading Issues in Economic Development, ed., G. Meier, Oxford University Press, New York.

Michaely, M. (1977), “Exports and Growth: An empirical investigation”, Journal of Development Economics, 4: 49-53.

Moschos, D. (1989), ‘Export expansion, Growth and the level of Economic Development: An empirical Analysis’, Journal of Development Economics, 30(1): 93-102.

Nidugala, G K. (2001), ‘Exports and Economic Growth in India: An Empirical Investigation’, Indian Economic Journal, 47(3): 67-78.

Phillips, P. C. B., and P. Perron (1988), ‘Testing for a Unit Root in Time Series Regression’, Biometrika, Vol. 75, pp. 335-46.

Ram, R. (1985), ‘Exports and Economic Growth: Some Additional Evidence’, Economic Development and Cultural Change, 33(2): 415-25.

──── (1987), ‘Exports and economic growth in developing countries: Evidence from Time-Series and Cross-Section Data’, Economic Development and Cultural Change, 36(1): 51-63.

Rodrik, D. (1999), The New Global Economy and Developing Countries: Making Openness Work, Overseas Development Council, Washington DC.

Serletis, A. (1992). “Export growth and Canadian economic development”, Journal of Development Economics, 38, 1 (January): 133-45.

Sharma, A., and T. Panagiotidis (2004), An analysis of exports and growth in India: Cointegration and causality evidence (1971-2001), ESRC Seminar Series, St Antony’s College, Oxford University.

Sinha, D. (1996), ‘Openness and Economic Growth in India’, Indian Journal of Economics, 77: 115-24.

Syron, R. F., and B. M. Walsh (1968), ‘The relation of exports and economic growth: A note’, Kyklos, 21(3): 541-45.

Toda, H. Y., and P. C. B. Phillips (1993), ‘Vector autoregressions and causality’, Econometrica, 61: 1367-93.

Tyler, W. G. (1981), ‘Growth and export expansion in developing countries: Some empirical evidence’, Journal of Development Economics, 9(1): 121-30.

World Bank (1993), The East Asian Miracle: Economic Growth and Public Policy, Oxford University Press, New York.