Liquidity Effects on the Term Structure of Government Securities Market in India - আরবিআই - Reserve Bank of India
Liquidity Effects on the Term Structure of Government Securities Market in India
Himanshu Joshi* |
An empirical examination of the term structure of interest rates in the Indian economy suggests cointegration (or long run stable relationship) among interest rates but existence of multiple common trends. The absence of unique common trend implies that long run movements of any one interest rate are not dominated by the movements of other interest rates. The presence of cointegration, however, suggests a long run interlocking of interest rates across markets and a possibility of their common response to changes in expectations about future monetary policy and/ or economic fundamentals. Finally, the results also suggest that structural policies pursued by the Central Bank could be of crucial importance in facilitating market integration. |
Introduction |
The process of deregulation of interest rates in Government securities market which began in 1992 has culminated into a full fledged market mechanism providing the much needed space for effective conduct of monetary and internal debt management policies in the Indian economy. Market determined interest rates were made applicable to government borrowings in gradual succession beginning with the auctions of 364 day Treasury Bills in April 1992, government of India (GOI) dated securities in June 1992 and 91 day Treasury Bills in January 1993. Later, as the primary market acquired greater depth, new instruments such as funded Treasury Bills, Zero Coupon bonds, Tap Stocks and Partly Paid Stocks, 14 days Treasury Bills and Capital Indexed Bonds were also introduced in keeping with the market's appetite. The changes in the scheme of financing of Government deficits have had important but mixed implications such as desirable reductions in monetized deficits, on the one hand, and an upward pressure on interest rates resulting in fiscal strains, on the other. Moreover, the introduction of several such instruments of different maturities meant the emergence of multiplicity of yields, resulting in rather complex term structure of interest rates. The problems associated with sharp variability of interest rates in the post reform period provide yet another dimension of the transition from a controlled system to a market regime. |
* | Dr. Himanshu Joshi is Assistant Adviser in the Monetary Policy Department of the Bank. The author is grateful to an anonymous referee for his comments on the paper. However, the usual caveat applies. |
The coupon rate on GOI securities of various maturities increased from the range of 10.50-11.50 in 1990-91 to 13.25-14.00 percent in 1995-96, but declined thereafter to the range of 10.85-12.15 percent in 1997-98. As a result, the weighted average interest rate on government dated securities moved in tandem from 11.41 per cent in 1990-91 to 13.75 per cent in 1995-96, and to 11.82 per cent in 1997-98. At the shorter end, 91 day Treasury Bills also showed considerable fluctuations, with the yield rate rising from 4.6 per cent in 1991-92 to an average of 12.67 per cent in 1995-96 but coming down sharply over the next two years to 6.83 per cent by 1997-98. A comparison of the yields on the short and the long ends in the government securities market reveals that the difference between the average yield of the 364 day Treasury Bill and 10 year government bond increased to 3.69 percentage points in 1997-98 from 2.18 percentage points in 1996-97 and 1.13 percentage points in 1995-96. |
The changing differences of yields among different maturities appear to arise not only from usual term premia but also from the asymmetric expectations over the short and long horizons. Yields on dated government securities in India are also influenced by call money rates or short term liquidity considerations in the money market (Rangarajan, 1997 and Reddy, 1998). Notwithstanding their sources the temporal variability and divergence among interest rates of different maturities are a potential cause of asset-liability imba-lances and unexpected portfolio losses for market participants. Again, to the extent that the term structure remains unstable, it becomes difficult for the Central Bank to extract market signals and use them for conducting forward looking monetary policy strategies. Keeping these aspects in view, this paper attempts to undertake an empirical assessment of the term structure of interest rates in the Indian economy in order to identify the possible regularities of relationship among various interest rates in government securities market. In doing this, the paper employs the well known cointegration and common trends analysis proposed by Granger and Gonzalo (1995). The technique allows for the identification of the reference rate underlying the movement of the overall term structure in the market. The common trends methodology has been in extensive use for analyzing the term structure in developed economies but rarely so in developing countries. In their original paper, Granger and Gonzalo (1995) provided an interesting analysis of the term structure of the US and Canadian securities and concluded the presence of one common factor in each country; both of which were themselves cointegrated thereby admitting a single common permanent component for the whole system. Some of the other notable applications are by Karfakis and Moschos (1990) and Hafer and Kutan (1994) who examined the long run relationship among short term nominal interest rates in the European Monetary Union (EMU) countries. More recently, Hafer, Kutan and Zhou (1997) analyzed the relationship between the long and short term interest rates for the EMU countries and concluded that even though common trends moved together in time, the German trend was hardly dominating. |
The rest of the paper is schematized in four sections. Section I provides a brief review of the notion of term structure of interest rates and discusses certain aspects related to the Indian economy. Section II gives a discussion on the data used in the study and the econometric methodology. Section III discusses empirical results. Finally, Section IV presents some concluding observations. |
Term Structure of Interest Rates : Indian Experience in the Post Reform Period |
The term structure of interest rates or the yield curve is the relationship between the redemption dates of various securities and their rates of return. Given the increased price risk inherent in long term securities, risk return analysis suggests that return should monotonically increase with the term to maturity. Expectations of market participants play an important role in shaping the term structure of interest rates in a financial market. Thus, if the investors are risk averse, and the interest rates on an average are expected to remain the same, longer dated securities will command higher rates of return than shorter dated ones. Conversely, the shape of the yield curve is reversed if interest rates are expected to fall with maturity (Hicks, 1939 and Malkiel, 1966). Equally integral to the evolution of the term structure is the expectation about the future rates of inflation as held in the classic study by Fama (1981) which argued that movements in interest rates essentially reflected fluctuations in expected rate of inflation. Fama's (1981) results were similar to those reported earlier by Nelson and Schwert (1977) and later by Mishkin (1981), Fama and Gibbons (1982) and Huizinga and Mishkin (1986) in the context of the post war US economy, except over 1979-82 when the Federal Reserve changed its operating procedures itself. Quite aside from expectations, investor preferences are also important in determining the shape of the term structure. Most investors, for instance, like to hold short term assets unless there exists a likable liquidity premium on long term investments. This is owing to preference for liquidity and ex ante assessment of risks by investors which are related to expected future changes in the nominal value of their investments (Hicks, 1939). This aspect was recently empirically investigated in the context of the US economy by Shen and Starr (1998) who concluded that the bid-ask spread (which reflects liquidity of the instrument) on Treasury Bills is priced in the bill market and accounts for a substantial portion of the term premium, sometimes to the exclusion of a risk premium in the term structure. Yet another theory of the term structure is based on the concept of 'preferred habitat' which maintains that although liquidity preference may not be the only guiding principle for all classes of investors, the investor's choice of maturity depends upon the his/her asset-liability management constraints. In this sense, while pension funds and insurance companies require long term, those such as banks would prefer to hold short term assets (Modigliani and Sutch, 1966). In practice, however, the term premia has been found to behave quite differently from what has been proposed by standard theories. Term premiums often behave irregularly on account of such factors as seasonalities, news and other unexpected changes in the economy. Subsequent research has considered factors ranging from expectations and risk preference to investment alternatives and individual preferences (Cox et.al,1985). |
Thus in light of the somewhat unclear position regarding the state of the yield curve theory, we propose to explore the nature of the link between the money market rates and yields in the Government securities in India. This is because exogenous/policy induced changes in liquidity are often seen to be driving Government bond yields.(1) For instance, comfortable liquidity situation in 1992-93 as a consequence of significant reductions in the CRR helped the RBI to raise Government borrowings at reasonable costs at a cut off yield of 11-11.42 percent on 364 day Treasury Bills and with a maximum coupon of 13.0 percent on dated GOI securities. Easiness in liquidity and call rates was also observed in 1993-94 which was reflected in the stability of cut off yields on Treasury Bills and coupons on dated GOI securities. However, in 1994-95 high call money rates reflecting tightening of liquidity resulting from asset liability mismatches in the wake of high demand for credit led to an across the board increase in coupon rates/cut off yields of government securities. Starting 1996-97, however, the yields began to soften owing to easing of call money rates as a result of the inflow of funds into the banking sector, aided partly by the spot forex purchases by the Reserve Bank of India and reduction in the statutory cash reserve ratio. A similar trend continued to prevail in 1997-98. Prima facie, there is therefore a significant link between the term structure of interest rates and changes in money market conditions. |
Methodology |
In order to elicit the long-run common link between interest rates in a term structure, we intend to follow the approach suggested by Gonzalo and Granger (1995). It is well known that if a given set of interest rate series are cointegrated then there exists an underlying nonstationary common long memory component. A term structure can have one or more common factors which can drive the complete range of interest rates under consideration. However, if the common factor is unique, then the reference interest rate can be easily identified. Even though the identification of this common factor will be the one of the key objectives of this exercise, it is also proposed to decompose each interest rate series into its permanent and transitory components and to study the interrelationships among them. In order to do this, we choose the following term structure of interest rates (i) very short term inter-bank call money rate or CALL (ii) cut off yield on short term 91 day Treasury Bills or TB91 (iii) cut off yield on medium term 364 day Treasury Bills or TB364 and, (iv) redemption yield on long term GOI dated securities or YTMGOV. The selection of interest rate on different Government securities as part of our term structure is dictated by the fact that all of these are not only market determined but represent the major chunk of trade in wholesale debt market (WDM). Government securities market then sets the tone for pricing in other debt markets. The analysis pertains to the period from January 1993 to February 1998. |
According to Gonzolo and Granger (1995), if a given set of time series are constrained by cointegration then it implies the presence of a non stationary common factor which is unobservable but can be recovered. It is this common factor which drives long run movements in the time series, thus resulting in cointegration. Symbolically, the common factor representation can be described as follows |
|
where [xt , yt] is a pair of integrated time series, (1,-A ) is the cointegrating vector and [ |
|
be a VAR (k) with n variables in vector Y, a constant m and white noise process |
While the matrix |
|
and finally solving the following eigenvalue problem |
|
for eigenvalues |
Trace = -T |
As cointegration is established, |
|
where an estimate of the orthogonal complement |
|
where |
Empirical Results |
It is customary to begin the analysis by recording the time series properties of the interest rates chosen to represent our term structure. Test statistics produced by the augmented Dickey-Fuller (ADF) unit root tests are presented in the Table below. |
Unit Root Test Statistics based on ADF Regressions |
Interest Rate | Levels | First Difference |
YTMGOV | -2.40 | -6.64* |
TB364 | -1.16 | -3.73* |
TB91 | -1.36 | -5.82* |
CALL | -1.62 | -7.82* |
Notes to Table : |
(i) | The tests pertain to models with a constant but no time trend. |
(ii) | A * denotes significance at the 5% level using the critical values of Fuller (1976). |
The unit root test statistics in the table indicate that all four interest rates are random walk or I(1) and, hence, amenable to cointegration. The empirical estimates of trace and maximum eigenvalue test statistics for testing the possible number of cointegrating vectors obtained from Johansen's (1988) procedure are presented in table below. |
Trace and Maximum Eigen-value Test Statistics for testing Cointegration Rank |
Number | Trace | Table value | Maximum | Maximum | ||||
of Co- | (estimated) | Trace (5%) | Eigen value | Eigen | ||||
integrating | (estimated) | value (5%) | ||||||
vectors | | | | | ||||
r = 0 | 106.43 | * | 53.3 | 70.62 | * | 28.1 | ||
r < 1 | 35.82 | * | 35.1 | 17.07 | 21.9 | |||
r < 2 | 18.74 | 20.2 | 14.11 | 15.7 | ||||
r < 3 | 4.63 | | 9.1 | | 4.63 | | 9.1 | |
Notes to Table : |
(i) | The statistics are obtained for a model without a linear trend in the non stationary part of the process. | |
(ii) | *denotes significance at 5%. | |
(iii) | The Table values of the test statistics are the 95 percent quantile of the asymptotic distribution of the test statistics. | |
(iv) | The diagnostics for the residuals from Johansen's VAR are as follows BP-Q(6) = 13.17, 6.93, 8.89, 8.68; ARCH(6) = 5.43, 4.22, 1.14, 3.26; J-B Normality = 0.067, 0.004, 13.626, 0.893. |
In the table although the estimated trace statistic suggests the presence of at least two cointegrating vectors, the maximum eigenvalue statistic suggests the presence of only one cointegrating vector at the customary 5% significance level. Both the estimated statistics, therefore, establish cointegration among the sample interest rates. In the table below we present a detailed account of the cointegration structure including the estimates of cointegrating vectors and the orthogonal complement |
The Profile of Cointegration Among Interest Rates |
Eigenvectors | ||||
YTMGOV | 0.53 | -0.40 | -0.35 | -0.29 |
TB364 | -3.97 | -7.12 | -5.03 | 3.81 |
TB91 | 5.89 | 6.31 | 4.61 | -2.64 |
CALL | -1.19 | -0.52 | -0.79 | 0.15 |
Eigenvectors | ||||
YTMGOV | -0.35 | 0.65 | -0.81 | -0.49 |
TB364 | 0.27 | 0.03 | -0.51 | -0.21 |
TB91 | -0.57 | 0.14 | -0.51 | 3.02 |
CALL | 0.68 | 0.24 | 0.70 | -2.57 |
Notes to Table : |
(i) | The eignevectors | |
(ii) | The common trends can be estimated as the linear combinations of the coefficients in the last 3 columns of the matrix |
Of interest is the plot of the transitory components of interest rate series that comprise the term structure depicted in the Graph. The movements of the transitory components in the Graph suggests that although components related to Treasury Bills were moving by and large in correspondence with that of the call money rate across the full range of sample, close interlinkages of yields on dated securities with the latter became distinct only since the middle of the calendar year 1996. Notably, peak to peak overlaps were clearly distinguished twice during September and January of the financial year 1996-97 when call money rates rose sharply owing to money market stringencies arising from quarterly advance tax payments (RBI, 1996-97). |
Eventually, a related question from the policy point of view is the extent to which liquidity management policy can actually influence the yields on Government securities. Contemporaneous OLS regressions between the transitory components of yields on securities and the call money rate suggest that a one percentage point rise in the latter can raise the yields in the range of 0.3 to 0.1 percentage point. More specifically, one percentage point average rise in the call money rate raises the yield on dated securities by 0.31 percentage point, TB 364 by 0.13 percentage point and TB 91 by 0.24 percentage point. All of these elasticities are statistically significant at 5% level. The explanatory power in the case of 91 TB equation (R2=0.54) is higher than that in the case of 364 TB equation (R2=0.32) and GOI dated securities (R2=0.15). |
Graph : Trends in Trasitory Components |
Concluding Observations |
Although the long, medium and short term interest rates representing the term structure of interest rates in this study are found to share a long run stable relationship, the absence of a unique common trend makes it impossible to identify a specific reference rate which may be expected to drive the overall spectrum of interest rates over the long horizon. It may thus, probably, be useful to enlarge the scope of analysis so as to include other interest rates, especially, those in other public and private debt markets for a comprehensive review of interest rates dynamics in the Indian financial markets.(2) On the other hand, the presence of cointegration among these interest rates is reassuring because it implies that interest rates in different markets and across various maturities are integrated and respond similarly to changes in expectations about economic policies and fundamentals. The empirical results presented in the study reveal that policy induced effects are readily transmitted across different markets in the short run. For instance, monetary relaxation has been quick to find its way to the yields on Treasury Bills. However, a similar correspondence between the yields on dated securities and the money market conditions became visible only after the first half of 1996 which coincided with several institutional developments such as the increase in the number of primary dealers in the call money market and their access to short-term funds. These policy initiatives seem to have promoted a higher degree of reactivity between the two markets thus underscoring the importance of structural policies in enhancing integration among various segments of the financial market. As the degree of integration in financial markets strengthens, the focus of monetary policy would shift to careful management of day to day liquidity in the money markets for ensuring stability in interest rates. |
Notes |
1. | In the most conventional model of monetary transmission, a shift in policy leads to a change in the money supply that, for a given money demand, leads to a change in money market interest rates. A key issue in this channel of transmission is how the changes in the interbank rate are spread to the entire spectrum of interest rate, in particular the long term interest rate pertaining to bonds. The effect is economically important because of changes that it brings about in bond prices and on the net-worth and debt to asset ratios of entities holding these bonds. For example, a restrictive monetary policy can depress asset prices and create cash flow and debt repayment problems leading to financial distress (Kamin et.al, 1998). |
2. | It may be mentioned that in this context, serious efforts will have to be undertaken for recording/collating high quality/frequency information from the concerned markets and their subsequent processing on a uniform basis, especially, developing appropriate weighted average rates for different transactions for purposes of decisive econometric analysis. |
References |
Cox, J., Ingersoll, J., Jr. and Ross. S., (1985): "A Theory of the Term Structure of Interest Rates", Econometrica, Vol. 53, 2. |
Fama, E.F., (1975): "Short Term Interest Rates as Predictors of Inflation", American Economic Review, Vol 65. |
Fama, E.F and Gibbons, M.R., (1982): "Inflation, Real Returns and Capital Investment", Journal of Monetary Economics, Vol 9. |
Huizinga, J and Mishkin, F.S., (1986): "Monetary Policy Regime Shifts and the Unusual Behaviour of Real Interest Rates", Carnegie Rochester Conference Series on Public Policy, Vol.24. |
Gonzalo, J and Granger, C., (1995): "Estimation of Common Long Memory Components in Cointegrated Systems", Journal of Business and Economic Statistics, Vol. 13, No.1. |
Hafer, R.W. and Kutan, A.M., (1994): "A Long Run View of German Dominance and the Degree of Policy Convergence in the EMS", Economic Enquiry, 32. |
Hafer, R.W, Kutan, A.M and Zhou, S., (1997): "Linkage in EMS Term Structures : Evidence from Common Trend and Transitory Components", Journal of International Money and Finance, Vol.16, No.4. |
Hicks, J.R., (1939): "Value and Capital", Oxford University Press. |
Johansen, S., (1988): "Statistical Analysis of Cointegration Vectors", Journal of Economic Dynamics and Control, 12. |
Kafrakis, C.J. and Moschos, D.M., (1990): "Interest Rate Linkages within the European Monetary System: A Time Series Analysis", Journal of Money, Credit and Banking, 22. |
Kamin, S, P. Turner and J. Van 't dack (1998): "The Transmission Mechanism of Monetary Policy in Emerging Market Economies: An Overview", Policy Paper No 3, Bank of International Settlements, Basle. |
Malkiel, B., (1966): "The Term Structure of Interest Rates", Princeton, Princeton University Press. |
Mishkin,F.S., (1981): "The Real Rate of Interest : An Empirical Investigation", Carnegie Rochester Conference Series in Public Policy, Vol 15. |
Modigliani, F. and Sutch, R., (1966): "Innovations in Interest Rate Policy", American Economic Review, May. |
Nelson,C.R and Schwert,G.W., (1977): "Short Term Interest Rates as Predictors of Inflation : On Testing the Hypothesis that the Real of Interest is Constant", American Economic Review, Vol 67. |
Rangarajan, C., (1997): "Activating Debt Markets in India", Reserve Bank of India Bulletin, October, 1997. Key note address delivered at the SBICAP Debt Market Seminar on September 5, 1997. |
Reddy, Y.V., (1998): "Interest Rates in India : Status and Issues", Reserve Bank of In-dia Bulletin, July 1998. Speech at the Inaugural Conference of Fixed Income Money Market and Derivatives Association of India (FIMMDA). |
Reserve Bank of India: Annual Reports 1996-97 & 1997-98, Mumbai. |
Shen, P and Starr, R.M (1998): "Liquidity of the Treasury Bill Market and the Term Structure of Interest Rates', Journal of Economics and Business, Vol. 50. |











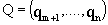 associated with the n-m+1 smallest eigenvalues. Given the estimate of
associated with the n-m+1 smallest eigenvalues. Given the estimate of 











