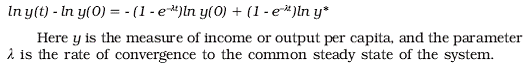IST,
IST,
Regional Inequalities in India in the 1990s: Trends and Policy Implications
We thank Development Research Group (DRG), RBI for the invitation to work on this project, and valuable inputs to progressing it at various stages. Participants at RBI seminars gave useful comments where a condensed version was presented. Interactions with RBI officers, during the course of the project, were a source of rich insights and contextual knowledge. We are particularly grateful to Dr. Rakesh Mohan, then Deputy Governor and Dr. Narendra Jadhav, then Principal Adviser and Chief Economist, Department of Economic Analysis and Policy (DEAP) for initiating this study, to Dr. Nishita Raje and Dr. Charan Singh, then Directors, DRG, DEAP for shepherding it through the long process of completion, to Shri Sanjay Hansda and Shri Ajay Prakash, then Assistant Advisers, DEAP for initial help and discussions with respect to the literature review and all DEAP Regional Offices for data support. We also acknowledge the useful comments of Dr. Laveesh Bhandari of Indicus Analytics on the first draft, as well as his significant help with the data. The opinions expressed here are those of the authors and not of the RBI, or any of the RBI officials acknowledged here. Jake Kendall’s work on this report was done while he was at University of California, Santa Cruz and does not reflect the views of the World Bank or any of its affiliated organizations. The authors are solely responsible for errors and omissions. Nirvikar Singh This study examines regional inequality in India with a particular focus on data below the state level. There are concerns that regional inequality in India has been increasing after the economic reforms that began in 1991. These concerns are supported by several statistical analyses, conducted mostly with state level data, which, however, does not reveal anything about what might be taking place within states. More disaggregated studies are typically qualitative or use only descriptive statistics. We tackle this gap in analysis by performing a systematic empirical analysis that admits of some causal interpretation. The main methodology is the use of cross-section growth regressions, which seek to explain longer run growth rates in terms of initial conditions of output and development. In turn, these regressions are derived from, and interpreted in the light of neoclassical growth theory, which in its basic form, suggests that diminishing returns to capital accumulation will drive convergence in income levels across geographic units. We use specific proxy measures for physical infrastructure, financial development and human capital, and the regressions identify the connections between these measures and growth. Hence, the study illuminates the role of aspects of physical infrastructure, financial development and human capital in influencing regional patterns of growth below the state level. In turn, this may have implications for government policies at the national and state levels. Using region and district level data, we find no evidence for divergence, but evidence for conditional convergence in some cases. At the region level, while partial measures of economic activity do not indicate any strong evidence for conditional convergence or divergence, there is clear evidence of conditional convergence in per capita consumption levels. Three points are noteworthy in these results. First, the convergence result is strongest for urban households. Second, the main significant conditioning variable is petrol consumption, which could be an indicator of the quality and quantity of road infrastructure (and which could also be related to access to urban areas). Third, dummy variables for the poorer states do not indicate that they were doing worse than the benchmark average state (Andhra Pradesh), though some of the regions with the largest negative residuals were in the poorer states. The district level results also indicate conditional convergence, but not absolute convergence. The conditioning variables used are measures of roads, literacy and credit, so the results are supportive of the importance of infrastructure and human development, as well as access to finance. These results are quite robust across a wide variety of specifications, and are consistent with a well-understood model of development, that emphasizes human capabilities and appropriate access to markets as determinants of growth. This study can be used to identify districts which require additional policy intervention along the three dimensions used, as well as districts where the performance is worse than the average, even after conditioning on development measures. In the latter case, social backwardness or policy implementation shortcomings may be the problem. The results for conditional convergence hold across states, as well as within most of the states in the sample, indicating that attention to improving these variables in districts where they are at relatively low levels can have a growth payoff, and improve the inclusiveness of growth, as measured by convergence of income levels across geographic regions. REGIONAL INEQUALITY IN INDIA IN THE 1990S: TRENDS AND POLICY IMPLICATIONS Nirvikar Singh, Jake Kendall, R.K. Jain and Jai Chander* 1. Introduction: Issues and Policy Relevance There are concerns that regional inequality in India has been increasing after the economic reforms that began in 1991. These concerns are supported by several statistical analyses, conducted mostly with state level data, which show that per capita state domestic products – already highly unequal – are moving further apart. However, state-level analysis does not reveal anything about what might be taking place in different regions within states. On the one hand, the state, as the main subnational political unit in India, is an appealing level of analysis. Intergovernmental transfers are decided in terms of allocations to the states, they have strong cultural identities, and they are strong political units, with considerable powers assigned to them by the Constitution of India. On the other hand, states are in some ways too large to allow a full understanding of regional patterns of economic activity and development. India’s larger states would rank high among the world’s countries, ranked by population. Even the medium-sized states have populations larger than many European nations. Many of India’s states are also quite heterogeneous, despite strong degrees of linguistic and cultural homogeneity. Within-state heterogeneity arises in characteristics such as geographic features, degree of urbanization, infrastructure, and human development. Solely focusing on differences in economic development across states misses these aspects of initial conditions and development potential and patterns. Of course, national government policy has recognized the need to operate at more decentralized levels. Administrative structures have long emphasized the district and taluk (block) as significant units of governance. In the last decade, major constitutional amendments have sought to develop more autonomous and effective local governments, both rural and urban. Nevertheless, systematic empirical examinations of regional inequality based on data below the state level have been extremely limited. This study seeks to correct this gap in existing empirical analysis, to provide a more finegrained, quantifiable understanding of trends in regional inequality in India. In some ways, this analysis fills a key gap between academic analyses and policy understanding. Policy makers and implementers often have a deep understanding of conditions at the ground level. Politicians and bureaucrats operate within their geographic regions of responsibility, and accumulate considerable local knowledge. Academics have examined data at the district level in India, but often focusing on description or summary statistics, rather than formal, empirically-based causal analysis. Causal analysis has been chiefly aimed at state level data, which is more easily obtainable. This study therefore uses disaggregated data to provide an empirical causal analysis that can be instructive for policymakers at the national and state levels. 2. Theoretical Framework and Empirical Methodology Our basic framework comes from the neoclassical economic theory of growth, which explains growth in terms of factor accumulation. If growth is expressed in per capita terms, and absent continual technical progress, diminishing returns to factor accumulation ensure that there is a long run steady state with constant per capita output, i.e., asymptotically, there is no growth in per capita output. Thus, economies starting with different factor endowments will converge to the same steady state, as long as there are no differences in technologies or other productive opportunities. If, instead, there is exogenous technological progress, then economies will grow at the rate dictated by this technological change. Typical neoclassical growth models (Barro and Sala-i-Martin, 1992, 1995) yield a loglinearization around the steady state of the form:
If there are persistent differences in technologies, then long run convergence to a steady state still takes place, but these steady states can differ, their characteristics being conditional on the differences in productive potentials. Where faster growth is also affected by other variables besides initial income levels, the convergence is said to be conditional: in other words, a poorer country (or region) may converge to a steady state that is different from that of the richer country (or region). Thus, one can identify three possible scenarios: absolute convergence, where different entities are moving toward the same steady state, conditional convergence, where they are converging to (possibly very) different steady states, and divergence, where there is no evidence of convergence. The last case is inconsistent with neoclassical growth models, but conceivably fits some endogenous growth models.1 Note that conditional convergence is quite consistent with increasing disparities across entities. Variables such as literacy, health and physical infrastructure may be the conditioning variables, as well as the economic policies followed. Clearly, the conditioning variables themselves may be endogenous. However, if one uses these variables at their initial values, they are predetermined over the growth period being studied, and one can posit a causal relationship. The empirical implementation of a convergence regression, allowing for the impact of different initial conditions, then takes the following form:
Studies of convergence across countries have focused on catching up by poorer nations through faster growth. While the evidence for any type of convergence across disparate countries is quite weak, one might expect greater possibilities for convergence across similar regions or constituent units of a federation such as India. One problem with this conjecture, however, is that India itself is extremely large and heterogeneous, and statelevel convergence regressions, even when restricted to the 14 ‘major’ states, are subject to some of the same potential shortcomings as cross-country regressions. As will be seen from a review of state-level studies in the next section, divergence across states may be a serious issue for India. At the same time, we have relatively little empirical knowledge of how patterns of growth have been shaping up at the level of geographic regions smaller than the states. 3. State-Level Convergence Studies In one of the first studies of convergence within India, Cashin and Sahay (1996), examined data for the period 1961-91, thus excluding the reform period of the last decade and a half, but including the Rajiv Gandhi reform period of the 1980s. The analysis is performed on 20 states, thus including some of the special category states, which receive central transfers according to different, and typically much more generous, formulae than the major states. This is important to note because the authors use state disposable income per capita, adding in all central transfers, except for shared taxes, to SDP. They find some evidence for unconditional convergence in the period of analysis, with the strongest effect being identified in the 1961-71 decade. These results are not changed in essence by controlling for other variables. Furthermore, the results indicate much slower convergence than that found across regions of developed countries such as the US and Japan. This meant that crosssectional dispersion of per capita incomes across states actually increased over the three decades studied, despite the inclusion of center-state transfers (though dispersion was greater when these were excluded). Cashin and Sahay also examine the role of internal migration in convergence, and find it to be weak. Several analyses followed Cashin and Sahay. Rao and Sen (1997) argue that the inclusion of four special category states in the Cashin-Sahay sample muddies their analysis. Furthermore, they argue that adding of transfers to SDP involves some double counting. Finally, Rao and Sen also take issue with the analysis of the equalizing effect of transfers, arguing that excluding shared taxes gives misleading results. Cashin and Sahay’s response, however, disputes these criticisms on empirical and conceptual grounds. Marjit and Mitra (1996) independently analyze a data set similar to Cashin and Sahay’s, but with different empirical methods: they argue that the evidence for convergence is weak. Ghosh, Marjit and Neogi (1998) also find evidence for divergence across states, over the period 1961-62 to 1995-96. Nagaraj, Varoudakis and Véganzonès (NVV, 1998) examine data on 17 states for 1970-94 (including three special category states). They find no evidence for absolute convergence. Using panel data (rather than a crosssection as in Cashin-Sahay) and per capita SDP (excluding transfers), NVV find that there is evidence for conditional convergence, with the conditioning being done on the share of agriculture and the relative price of agricultural and manufactured goods. Adding infrastructure indicators substantially strengthens the estimated rate of conditional convergence. While NVV do not explicitly consider transfers, they emphasize the importance of infrastructure2 and non-measured political and institutional factors (captured in state fixed effects) in explaining differences in steady state growth rates across states. To the extent that center-state transfers have a potential role in affecting these determinants of growth, they are important in this analysis. Rao, Shand and Kalirajan (RSK, 1999) examine data for the 14 major states, for the period 1965-95, using SDP as the output measure. RSK find evidence for absolute as well as conditional divergence, a result that is quite robust across sub periods as well. They suggest that the speed of divergence increased in the last half-decade of their sample. However, this does not seem to be the decisive factor in explaining the difference from Cashin-Sahay: instead, the exclusion of special category states, and of centerstate transfers are of greater importance. The differences in conditioning variables and estimation methodology from NVV (who use a fixed-effects panel model) may explain the difference in conditional convergence results between RSK and NVV. RSK emphasize the role of private investment in explaining growth differences across states. They find that private investment goes disproportionately to higher-income states, as well as to states that have higher per capita public expenditures.3 RSK also argue that explicit center-state transfers have had moderate impacts on interstate inequalities, and that these effects have been outweighed by implicit transfers through subsidized (public and private) lending and through interstate tax exportation. Two other similar studies of possible convergence among India’s states are those of Bajpai and Sachs (1999) and Aiyar (2001). The former study examines data for a sample of 19 states for 1961-93. For the sub-period 1961-71, they find some evidence of convergence, but not for later subperiods or for the period as a whole. Allowing for conditional convergence does not qualitatively alter these results. Aiyar also uses the 19-state sample, for 1971-96. He finds weak evidence of absolute convergence for the 1970s, but divergence for later sub-periods (especially the 1990s), as well as for the overall period. He estimates a panel with fixed effects, as do NVV, in which he does find evidence of conditional convergence. His conclusions are similar to those of NVV and RSK, emphasizing the importance of infrastructure, private investment, and non-measured institutional factors. Singh and Srinivasan (2005) examined the effects of foreign direct investment (FDI), as well as credit availability, in state-level convergence regressions (Table 1). They obtain several interesting results. First, the evidence for convergence or divergence is inconclusive, since the coefficient of base-year SDP is never significantly different from one.4 Second, any one of the financial variables taken individually is estimated to have a significant impact on growth of SDP. When two or more financial variables are included, there is evidence of multicollinearity, but otherwise the results are robust. They are consistent with a story where domestic and foreign capital are complements, and with data on credit-deposit ratios and of FDI approvals (both suggesting greater regional concentration of credit and investment),5 the evidence is suggestive of mobile domestic and foreign capital driving growth.
Adabar (2005) uses data for the 14 major states of India from 1976-77 to 2000-01 and employs a dynamic fixed effects panel growth regression. Once per capita investment, population growth and human capital, along with state-specific effects are controlled for, he finds evidence of conditional convergence at the rate of about 12% per five-year span. Purfield (2006) also uses dynamic panel estimates with data for the 15 largest states for 1973/ 74–2002/03 (averaged over six non-overlapping five-year periods). She finds slow absolute convergence, somewhat faster conditional convergence, and, somewhat surprisingly, negative impacts on growth of the size of state government.6 Some of the other results are also puzzling, illustrating the difficulty of reaching definitive conclusions with state-level data. 4. Inter-State Inequality in India: Additional Perspectives Ahluwalia (2000) examines the most recent data on the performance of India’s states. He uses the Gini coefficient for the 14 major states, and finds that interstate inequality, after being stable for most of the 1980s, increased, starting from the late 1980s, and even more in the 1990s. Many of the factors that he identifies as affecting growth performance are those emphasized earlier by NVV and RSK, suggesting that the fundamental situation that India faced earlier in the reform period has persisted through the decade of the 1990s.7 Ahluwalia (2001) adds some simple regressions to his earlier analysis, but these do not change the overall analysis or conclusions.8 Dasgupta et al (2000), covering a period from 1960-61 to 1995-96, find a clearly diverging pattern amongst the states in terms of the coefficient of variation of per capita SDP as also the growth in per capita SDP. In terms of the rank correlation matrix (in respect of per capita SDP) as also the index of rank concordance, the position of states turned out remarkably stable for any chosen pair of years. The sectoral contribution, viz., from primary, secondary and tertiary sectors, to the overall divergence indicates that the divergence between states is least in terms of infrastructural development and largest with respect to agriculture. Considering the structural features defined in terms of sectoral shares, this study has, however, brought out a case against divergence. Based on a careful review of a multitude of factors relating to demographic indicators, female literacy, SDP, poverty, development and non-development expenditure by state government, shares in plan outlay, investments, banking activities and infrastructure development, Kurian (2000) argues that the accelerated economic growth since the early 1980s with increased participation by the private sector has aggravated regional disparities. The ongoing economic reforms since 1991, with stabilization and deregulation policies as their prime instruments and a very significant role for the private sector, seem to have further accentuated the disparities. By using a non-parametric kernel density for poverty estimation, Dhongde (2004) decomposes the changes in poverty across regions for the year 1999-00 and observes that differences in state and national poverty levels were largely explained by differences in the state and national mean income levels rather than differences in the state and national distributions of income. An important policy implication of the study is that states with extremely high levels of poverty would have reduced poverty significantly by raising their mean income levels to the national mean income, instead of changing their distribution of income to match the national income distribution. In other words, growth toward the average income level is more important for poverty reduction than redistribution toward the average distribution. Lall and Chakravorty (2004) suggest that spatial inequality of industry location is the primary cause of spatial income inequality in developing nations. In this context, the contribution of economic geography factors to the cost structure of firms in eight industry sectors in India was examined and the local industrial diversity was found to have significant and substantial cost reducing effects. Since new private sector industrial investments in India are biased toward existing industrial and coastal districts while state industrial investments (in deep decline after structural reforms) are far less biased toward such districts, the study concludes that structural reforms lead to increased spatial inequality in industrialization, and therefore, in income. Dholakia (2003) has examined the trends in regional disparity in economic and human development in India over the last two decades. His study points out that while per capita income does not show any significant trend in regional disparity over the last two decades, seven out of nine human development indicators display a declining trend in regional disparity. Similarly, 12 of the other 16 related social and human development indicators show a marked decline in regional disparity during 1981-91. The concept and measurement problems involved in Indian data on state domestic product are briefly discussed in Dholakia (2003) to point out the limitations of past studies on the subject. In a cross-sectional setting, Granger causality or precedence is tested by considering lags in the independent variable and interchanging the variables. Using this method, Dholakia (2003) finds a two-way causality between human and economic development. The structure of the relationship was found to be varying over time when human development indicators (HDIs) are the cause and per capita SDP is the effect, but in the reverse causality case, the structure of the equations is stable over time. Moreover, HDIs have been found to positively influence per capita SDP with a lag of about eight years, whereas per capita SDP affects the HDIs within two years. Therefore, according to this analysis, emphasis on economic growth is likely to address the issue of twin disparities in income and human development in the shortest time. This analysis also suggests that emphasis on human development in states may lead to the postponement of rapid economic growth and also to some inefficiencies cropping up in the delivery of output, resulting in a further shifting of the structure of relationship between per capita SDP (effect) and HDIs (cause).9 Jha (2000) examines the empirical relationship between economic inequality, poverty and economic growth in the Indian states. Gini coefficient, real mean consumption and the head count ratio for rural and urban sectors and average for 14 major Indian states has been computed using NSS data on consumption for the 13th to the 53rd Rounds. The study finds that there is (conditional) convergence (in terms of levels) in inequality and poverty measures across states. The coefficients of variation do not show any tendency to fall over time. Based on the observation of a rising coefficient of variation of the rural head count ratio, the study points towards greater dispersion in rural poverty across states over time. Inequality was found to be acting as a constraint on growth in the states with high Gini coefficients as well with poor growth performance. Therefore, the author recommends that economic growth should be used for reduction of inequality and poverty. For equitable distribution of consumption, he suggests widespread tax reform to increase tax revenues and economic growth and make the tax structure more redistributive; improvement of efficiency of public expenditure and of the social safety net; and design of a good social sector policy framework promoting agricultural growth as opposed to nonagricultural growth, protecting the poor from the effects of macroeconomic shocks and building up of pressure groups of the poor. 5. Regional Inequality: Disaggregated Studies Kurian (2000) has examined intra-state disparities and drawn attention to the fact that the newly created states develop faster than the pre-partition states. The study highlights a few successful cases where intra-state regional disparities were reduced considerably through public policies such as in Malabar region (Kerala), drought-prone districts of Haryana and the remotest villages of Himachal Pradesh. Tamil Nadu was identified as the most successful state in reducing intra-state disparities even with substantial variation in natural endowments across different parts of the state. In an attempt to estimate the district health accounts in Karnataka for the year 1997-98, Annigeri (2003) observes that in terms of sources of funds, private funds account for about 52 per cent of the resources flowing into the district. Interestingly, both state and union governments are found to have spent less on medicines than on salary. Gulmoto and Rajan (2002) have provided district level indirect estimates of birth and fertility rates for all districts of India using population aged 0-6 years as observed in 2001. While the fertility is lower than 3 children per woman for the southern and coastal states along with Punjab, Himachal Pradesh, Tripura and Manipur, high fertility districts (i.e., with more than 5 children per woman) are still widespread in north India. Nonetheless, there is evidence to believe that India is passing through the last phase of fertility transition, moving towards moderate to low fertility. Debroy and Bhandari (2003) identify 69 backward districts based on six indicators, viz., poverty ratios, hunger, infant mortality rate, immunization, literacy rate and enrollment ratios. Sources of data include both primary and secondary sources. Each indicator throws up a set of districts. Based on poverty ratios, they find that backward districts are present, apart from the BIMARU states (Bihar, Madhya Pradesh, Rajasthan and Uttar Pradesh),10 in Gujarat, Maharashtra, Karnataka, Tamil Nadu, Andhra Pradesh, Orissa, West Bengal and the North-East. Hunger has a similar spatial distribution with less universality and more concentration in the East and the North-East. Backward districts based on infant mortality rates are concentrated in the BIMARU states and Orissa with some presence in Karnataka and Andhra Pradesh. Lack of immunization was found to be prevalent in the BIMARU states. Districts with low literacy rates and enrollment ratios are found to be spread all over the country. Given that each indicator selected a different set of districts, a backward district has been defined by them as one which is backward as per four out of the above six indicators. The 69 districts so identified are distributed as follows: 26 in Bihar, 13 in UP, 10 each in Jharkhand11 and Orissa, 6 in Madhya Pradesh, 3 in Arunachal Pradesh, and 1 in Karnataka. Debroy and Bhandari (2003) observed that connections between 69 backward districts and the rest of the economy are grossly inadequate, with poor national highways, state highways and railway networks. Poor infrastructure deters the private sector, making development dependent on public funds. Flood problems in Bihar, UP and Orissa are also considered as the cause for their backwardness. Thus, addressing these two issues among others is crucial for uplift of these backward districts. As we shall see in subsequent sections, our district-level analysis provides a quantitative analysis of the the linkages informally explored by Debroy and Bhandari. Using the estimation procedure of the NSS 55th round on variables for monthly household consumer expenditure and household size, Sastry (2003) has made district level poverty estimates, and shows that it is feasible to derive valid distributions for a majority of districts on the basis of Relative Standard Errors criteria. Finally, Singh et al. (2003) use NSS region level data to examine issues of convergence, though performance has to be measured by alternatives to income, which is not available at this level of disaggregation. This kind of data forms the basis for part of our analysis, and is discussed further in the next section. 6. Data Description and Summary Indicators We use two sets of data for the analysis conducted in this report. First, we use data from the National Sample Survey (NSS), which is at the level of agro-climatic regions. There are 78 such regions in India, but we have complete data for 59 regions, which forms the basis for the analysis here. This analysis extends the work of Singh et al (2003). The data used here include six variables: consumption expenditure, petrol sales, diesel sales, bank credit, bank deposits and cereal production. Consumption expenditure provides the broadest measure of economic activity among these. There are issues with respect to differences in data collection methodology across rounds, but we believe the analysis is still valid. In particular, since we are examining cross-sectional variation in growth rates, rather than time trends, data collection methodology changes are less important, and less likely to be a source of bias. The most novel aspect of the analysis performed here is the use of district level data to conduct a convergence analysis of growth. We use data on district level domestic product (DDP), along with data on population, road kilometers, literacy rates, and credit and deposit levels. DDP data was obtained from individual state governments, credit and deposit levels from RBI regional offices, and the other variables from the Indian Census. The main data constraint was in availability of DDP data, and this restricted us to nine states. The relevant states are highlighted in Table 2, with some summary statistics. The nine states covered account for over 60 percent of the country’s population and domestic product.12 The sample states are on average slightly above the national average per capita NSDP. There is also some regional variation in the sample, although with relatively greater coverage of the southern states (4), followed by northern states (3) and one each from the west and east. Maps of the states with districts named as in 1991 are shown in Appendix 1. The data used are for 1991 and 2001, allowing a ten-year snapshot of growth across the districts in our sample.
There are issues of comparability across states in DDP data, but this is addressed to some extent by analyzing the data state by state (in addition to pooling across states). Indira et al. (2002) looks at the ‘far from settled’ conceptual and availability issues of data on income and poverty estimates at the district level. It is based on discussions at a UNDP sponsored workshop in July 2001 to develop a common methodology for calculation of district level income and poverty estimates. Some issues that were debated and discussed are as follows. While some states limit district income to commodity producing sectors (‘district product’) others include non-commodity producing sectors as well (‘district income’). Animal husbandry needs to be clubbed with agriculture. District level prices need to be developed. Estimation of services is very difficult due to no estimates of income accrued in a district. Remittances from another state need to be distinguished from remittances from abroad. Thus, for various conceptual differences, DDP across states may not be strictly comparable. Issues relating to the definition, database and methodology to be used for estimation of poverty at the district level are also far from settled. Despite the data comparability and other measurement issues, we would argue that district-level analysis still has validity. Certainly, individualstate regressions avoid issues of comparability across states. To some extent, comparability can also be handled by including state dummies in pooled regressions. Overall, we would argue that even imperfect measurement is better than none at all, and to the extent that biases in data can be identified, one can also point out potential biases in the results. Methodologically, it is also worth noting that measurement error in the dependent variable (here, DDP, which is most subject to data problems) does not lead to biased coefficients, only to greater imprecision. The omission of relevant explanatory variables in the regressions may therefore be a greater practical source of bias. 7. Analysis of NSS Regional Data The NSSO divides the Indian states into 78 homogenous agro-economic regions that are groups of contiguous districts, demarcated on the basis of agro-climatic homogeneity. Each region is contained within a state or union territory. Together these regions cover all of India. For each region, Bhandari and Khare (2002) constructed an economic performance index based on five variables: petrol sales, diesel sales, bank credit, bank deposits and cereal production. They compared the years 1991-92 and 1998-99, and reported how each region did over this period, in terms of share of the overall economy. The Bhandari-Khare calculations revealed several interesting patterns. First, a clear West-East divide emerges in their analysis, with the West increasing its economic share. Second, there is no obvious North-South or coastal-inland divide. Third, most of the regions that do the best are centered on urban areas, which appear to be acting as growth poles. Fourth, many of the areas that lag are rain-fed agricultural regions, consistent with the general consensus that agriculture has been bypassed by the reform program to date.13 Fifth, Punjab, Haryana and Kerala do relatively well in this analysis (better than when per capita SDP is used as a measure of performance), consistent with a possible impact of international remittances for these states. Finally, while some states are doing consistently well, in terms of all regions within the state increasing their relative share (e.g., Karnataka, Kerala, Punjab and Haryana), there are other states with marked internal disparities in regional performance (e.g., Andhra Pradesh, Madhya Pradesh and Maharashtra). Thus, going down to the NSS region level provides a considerably more nuanced picture of the geographic patterns of economic change in the post-reform period. Singh et al (2003) performed convergence analysis using the five individual components (diesel consumption, petrol consumption, credit, deposits, and cereal production) of the Bhandari-Khare index. Due to data gaps, 59 of the NSS regions were used for the regressions, covering all the 14 major states, plus Assam and Himachal Pradesh. Thus, the coverage at the region level exceeds what we are able to achieve in subsequent sections at the district level, which, on the other hand, provides greater disaggregation. Therefore, this tradeoff further justifies analysis at both levels. In the absence of dummies, growth of credit and diesel consumption show evidence of absolute divergence, while only the latter result persists when conditioning variables are included. Including zonal dummies for north, west and south completely removes any absolute or conditional divergence effects, but the three zonal dummies are all statistically significant (except in the case of cereal production), indicating otherwise unexplained differences in the growth processes across these zones of the country. Here we present a more detailed examination of interstate variation by including state level rather than zonal dummies. Andhra Pradesh is used as the base state, and its dummy variable is therefore omitted. The results are summarized in Table 3, with standard errors reported in parentheses below coefficient estimates. Statistically significant positive and negative coefficients (excluding the constant terms) are marked in blue and yellow respectively with asterisks. Of the five variables used to measure economic activity, two, namely petrol consumption and cereal production (each in per capita terms), indicate statistically significant evidence of conditional convergence. In each of the regressions, none of the economic variables used for conditioning are statistically significant, indicating that the initial conditions that influence growth performance are not being captured in this data set. The chief variables of interest, however, are the state level dummies. In a cross-section regression with state-level data, there is limited scope to include such dummies. Here, we are able to examine the entire pattern of base-level growth differences across the states with dummies. We use Andhra Pradesh as the control state, as it is a state with an intermediate growth performance in the period under examination. Hence, each state dummy represents growth performance compared to Andhra Pradesh, controlling for all measurable effects with the data available. According to this criterion, we see that Assam, Orissa and Bihar are by far the worst performers among the states in the sample. All these states are in Eastern India. Orissa has statistically significant (at least at the 5% level) negative coefficients for all five of the variables, while the other two states have statistically significant coefficients for four of the variables – excluding deposits for Assam and cereal production for Bihar – though in each case the coefficients are still negative. For each of Madhya Pradesh, Rajasthan and Uttar Pradesh, petrol consumption and credit are both negative and significant. Diesel and petrol consumption are both negative and significant for West Bengal. Gujarat, Haryana and Maharashtra each have a single negative and significant dummy coefficient among the five regressions, without any positive and significant coefficients. In the case of Kerala, the dummy in the cereal production regression is negative and significant, while the coefficient for the petrol consumption regression is positive and significant. The only other positive and significant coefficients are for Punjab in the cereal production regression, and for Himachal Pradesh in the diesel and petrol consumption regressions and the deposits regression. Overall, therefore, the picture that emerges from these regressions is consistent with the view of the Eastern states and the BIMARU states as the worst performers in terms of economic growth. The caveat to this observation is that each individual performance measure only provides a very partial indicator of economic activity. Further understanding of the growth performance of regions comes from examining the residuals for the different regressions. Table 4 summarizes the five best and worst performing regions in terms of magnitudes of negative residuals. A large negative residual indicates that a region does worse than would be predicted by the explanatory variables in the regressions. There is some degree of pairing among regions within states, for best and worst regions. This is a consequence of the inclusion of state level dummies in the regressions. However, the presence of certain states and not others within these extreme residuals is perhaps indicative of greater disparities within these states relative to other states. Other possible factors are the size of the state (larger states being more heterogeneous, with more regions) and greater heterogeneity independent of size (e.g., Maharashtra may be especially heterogeneous in terms of urbanization and climatic variety). Perhaps the most important observation is to note that some regions are among the worst performers, even controlling for the states they are in. In particular, Orissa is the worst performer in terms of credit and deposits, with the largest negative dummy coefficients, and Coastal Orissa is the worst performer, even beyond the state average. Other cases of extreme outliers appear to be Southern Orissa for diesel consumption, and Western Haryana for petrol consumption. We also have data on personal consumption expenditure from the 50th and 55th rounds of the NSS, for rural, urban and all households.14 While these data are for 1993-94 and 1999-2000, they can be used to perform convergence regressions with the same conditioning variables that were used above. We present a sequence of results with this data. We also explore one additional alternative in this case, calculating credit and deposits as ratios of consumption expenditure in addition to using them in per capita terms. This is more in line with typical measures of financial development as used in the literature on cross-country growth convergence. Estimation is carried out with linear regression allowing for heteroskedasticity-robust errors.
Table 5 presents results using the base specification, with credit and deposit estimated as per capita figures. For all households, the conditional convergence coefficient is negative and statistically significant, but small in magnitude, indicating slow convergence. The financial variables are insignificant, while the measures of economic activity captured in petrol and diesel consumption are the correct sign, and, in the case, of petrol, significant. The coefficient of cereal production has the wrong sign, and is marginally significant. For rural households alone, the evidence of conditional convergence is weaker. The financial variables have the wrong signs from what would have been expected (though this may be consistent with overall credit in a region being more reflective of urban credit). The other variables have coefficient signs, magnitudes and significance similar to the regression for all households. For urban households, the evidence for conditional convergence of consumption expenditure is somewhat stronger, and the financial variables have signs more in keeping with expectations (the negative sign for deposits is similar to that for district level data, and is discussed in the next section in that context). Table 6 presents alternative results where the financial variables are calculated as ratios of consumption expenditure: some approximation is involved there because we use 1991 population data available to us rather than 1993 or 1994 data, to convert per capita consumption figures to totals. The scaling allows one to capture the idea that financial variables may simply track standards of living as measured by consumption, and provides a robustness check since some of the financial variables in Table 5 have signs opposite to what would have been expected. The results in Table 6 are qualitatively similar, however, suggesting that they are not sensitive to the particular specifications of the financial variables. Tables 7 and 8 present corresponding results for the two different specifications in Tables 5 and 6, but now include state-level dummies as well. The conditioning variables have effects roughly similar to the previous regressions. As one would expect, now the conditional convergence speeds are somewhat higher, as a result of controlling for different base growth rates through the state dummies. The omitted dummy is for Andhra Pradesh. Only one of the state dummies is significant for urban households, but several are significant for rural households, and that holds true even more for the combined data. This is suggestive that differences across states in growth of per capita consumption expenditure – controlling for initial conditions – are greater for rural households. We once again examine the outliers in terms of residuals, to see if there is any discernable pattern among the regions, after controlling for the measured factors we have used. These results are presented in Table 9. Comparing this with Table 4, we see that the pattern of best and worst districts is quite similar for consumption expenditure as for the other variables measuring economic activity. In this case, one has the additional finding that the overall results are driven in most cases by the performance of the rural economy – this is exactly what one would expect at this level of geographic aggregation, and is a result that is difficult or impossible to obtain with state-level data. We can summarize the results for the region-level data as follows. We estimated convergence regressions using various measures of economic activity such as petrol and diesel consumption, bank deposits and credit, and cereal production. These partial measures indicate no strong evidence of conditional convergence or divergence across the 59 agro-climatic regions covered in the sample. However, several states have significantly negative dummy coefficients, indicating that their performance is markedly below that of the benchmark state (Andhra Pradesh), and these states are chiefly the poorer ones of Bihar, Orissa and Uttar Pradesh. In these regressions, the financial variables are not significant explanators of performance. We are also able to identify regions which are the worst performers in the sense of being furthest below the regression line (and therefore doing worse than would be predicted based on initial conditions as measured): these are chiefly, though not exclusively, in poorer states, or likely to be poorer regions of states. Similar regressions are performed for region-level data, using per capita consumption expenditure as the dependent variable. Consumption expenditure is an appealing measure of well-being, though it is not the outcome variable that fits with the standard growth model – that would be income, which includes saving as well. Interestingly, in contrast to simple inequality measures, which suggest that urban inequality has been increasing, here we find that the strongest conditional convergence effect occurs for urban households. There is weaker conditional convergence for rural households, but for all households the convergence result is still quite strong. Of the conditioning variables, the only strong and clear effect comes from initial petrol consumption, which may plausibly be an indicator of the quality and quantity of road infrastructure in the regions. This result can therefore be considered in conjunction with the impact of road kilometers per capita, to be considered in the district-level regressions. The financial variables are either insignificant, or sometimes have the wrong signs (compared to what would be expected) for rural households – this might be an indication of problems with channeling credit to rural areas for improving standards of living, or it may simply be an indicator that bank credit is not meant to improve rural consumption outcomes. Nevertheless, the negative and significant coefficient bears further investigation. In terms of state-level performance relative to the benchmark, the signs of the dummy coefficients are now actually less of a cause for concern: there are no negative and significant coefficients, and some of the poorer states have positive dummy coefficients. The worst regions in terms of residuals, however, do seem to be similar to the regressions with partial measures of economic activity. 8. District Level Analysis : Pooled Results We first performed a convergence analysis for the entire data set, which consists of 210 districts spread across nine states.15 In addition to the benefits of disaggregated analysis, there is a significant econometric advantage to working with district level data. Districts are much more homogeneous in size than are the states themselves. Hence, a cross-sectional analysis with district level data avoids the problem of unevenness in the underlying size of the units represented by different observations.16 While the pooled regressions constrain the coefficients to be equal across states, we can test for differences in error variances, and estimate the convergence regression with some form of generalized least squares (GLS). To mitigate various forms of heteroskedasticity, we employ Huber-White (robust) estimates of variance in some specifications. A likelihood ratio test rejects the null hypothesis that all the states in the sample have the same error variances. Hence we also employ the clustered, robust error estimator where the error variances have been clustered at state level. The basic absolute convergence regression is presented in columns 1 and 2 of Table 10. Column 1 features estimates using robust standard errors, while column 2 features clustered, robust errors. In particular, the estimates in the second method are robust to any type of correlation within the observations of each cluster (i.e., state). We present both sets of estimates to check the robustness of our results. The results suggest no statistically significant indication of absolute convergence or divergence at the usual significance level. In general, we find that the coefficients across the two estimation methods (robust and robust cluster) are not qualitatively different in sign and statistical significance. It should be noted that the explanatory power of the absolute convergence regressions is extremely low: clearly, initial conditions beyond initial income levels matter for predicting future growth. Later, we also perform regressions with state-level dummies included, to allow for differences across states in the base growth rates (as captured in the constant terms of the regression), while still restricting the impacts of initial conditions to be the same across states. Table 10 (column 3) also presents results for absolute convergence, allowing for differences across the states. This is accomplished by including state level dummies to capture differences in base growth rates. The dummy for Andhra Pradesh is omitted, so it serves as the benchmark state. The results indicate significantly higher base growth for Karnataka and Tamil Nadu, and lower base growth for Rajasthan and Uttar Pradesh, relative to the benchmark state. Allowing for state dummies, even though it imposes the restriction that all states have the same convergence rate, increases the estimated convergence rate substantially, as well as dramatically increasing the explanatory power of the regression. The results in Table 10 illustrate the value of the disaggregated approach pursued in this analysis, since state-level regressions impose the restriction that the base growth rate is the same for all the states.17 It should be noted that allowing for state-level dummies also addresses to some extent data definition differences across the states. Hence, the low base growth rate for Uttar Pradesh may be partly due to data issues. However, without further data collection and analysis, it is impossible to isolate this effect. It is also possible to extend the assumed differentiation across states further, by including interaction terms as well as state dummies. Table 11 presents results for absolute convergence, with state level dummies, and interacting these dummies with initial year DDP per capita (in logarithms), to capture differences in convergence speeds. In this case, rather than omitting Andhra Pradesh, we omit the overall constant term for symmetry, so that each state has dummy coefficients. Allowing for differing convergence rates across states changes the earlier results quite a bit. The results in Table 11 indicate higher base growth for Punjab, and to some extent Andhra Pradesh, Maharashtra and Rajasthan. The interaction terms indicate faster convergence for Punjab and Rajasthan, and to some extent Maharashtra, but also suggest weak evidence for divergence of districts within Tamil Nadu. Note that this regression is similar in effect to running separate regressions for the individual states, which we also present later in the report, but it imposes additional restrictions on the error structure, vis-àvis single-state regressions. The results in Table 11 further illustrate the value of the disaggregated approach pursued in this analysis, since statelevel regressions impose the restriction that the convergence rate is the same for all the states. Next, we turn to conditional convergence regressions. These regressions, by using conditioning variables other than initial year DDP per capita, provide information on what aspects of initial conditions are supportive of growth, and what their impact may be. We use three categories of conditioning variables. First, we include district road kilometers as a measure of physical infrastructure. To allow for differences in area across districts, we normalize the total road kilometers by the district area. Second, we include literacy rates as a measure of human capital. Third, we include either credit per capita and deposits per capita, or a single credit-deposit ratio, in either case measuring district-level availability of financial capital or financial development. Another way to think about our conditioning variables is in terms of access to key aspects of economic activity. The road variable potentially measures access to markets, the literacy rate can be thought of as measuring access to jobs, and the financial variables capture access to credit. We would expect all the conditioning variables to have positive impacts on the level of economic growth. Table 12 presents GLS (with the standard heteroskedasticity adjustment) results, as well as the results of cluster regressions: the alternative methods allow us to check robustness of the results across different assumptions on the error terms. The table also presents results from two different specifications of the financial variables. The two methods give the same coefficient estimates, but different sizes of standard errors. Estimates from both methods indicate conditional convergence, with the rates of convergence being very high: 35.5 percent and 20.7 percent respectively. This finding is in stark contrast to most state level studies, which find little or no evidence for conditional convergence, and never such rapid convergence. Note, however, that the sample excludes the states of Madhya Pradesh, Orissa and Bihar,18 where some of the most persistent pockets of poverty and underdevelopment are located. Thus the positive result with respect to convergence is not contradictory to other studies; rather, it suggests that problems of growing regional inequality may be geographically quite concentrated. The conditioning variables in Table 12 mostly have the expected signs. The density of road kilometers is not significant, but the literacy rate and the credit per capita are positive and significant at the 5 percent level or better. Thus, districts with greater human capital, and access to credit grew faster, according to these regressions. The methodology does not allow one to distinguish which of these factors might be most important – however, it is a plausible position that all of them go hand-in-hand in affecting growth. The negative coefficient on the deposits per capita is not consistent with the hypothesis that it measures one aspect of overall financial development. However, the variable may be proxying for an effect where a district is unable to absorb funds locally, as a result of other constraints. When the specification is modified to using the credit-deposit ratio as a sole measure of credit access and/or financial development, it is positive and significant. In fact, the significance of the deposits per capita variable, and the minor puzzle of its negative sign, disappears when state level dummies are allowed for. Those results are presented in Table 13. Now the conditional convergence rate across districts is even higher, while the measures of financial access and human development all remain positive and significant. The measure of market access is marginally significant and of the wrong sign in the first specification, but this result is not robust to the alternative specification for the measure of financial access. The omitted state dummy is for Andhra Pradesh, which had an intermediate rate of growth in this period, among all the major states. Several of the state dummies are significant: Karnataka has a significant positive dummy coefficient (i.e., a base growth rate above that of the benchmark state, Andhra Pradesh), while Kerala, Maharashtra, Rajasthan and Uttar Pradesh have significant negative coefficients. There is still a minor puzzle in the Table 13 results, in that the variable measuring access to roads (road km. divided by district area) is negative and now also statistically significant in the first specification, with two separate financial development variables. To examine the sensitivity of our results to the specification of the roads variable, we also estimated the equations in Tables 12 and 13 using total road kilometers instead (in logarithms). These results are presented in Tables 14 and 15. It may be seen in Table 14 that the alternative roads/ access variable is always of the expected sign and statistically significant, supporting the conjecture that access to roads matters for economic development. It is also the case that none of the other coefficients are qualitatively affected by the new specification of the roads variable, since the magnitudes and statistical significances are essentially the same as in Table 12. Some coefficients are higher (e.g., literacy), and some are lower (e.g., credit in the first specification), but these differences are not economically or statistically significant. In Table 15, compared to Table 13, the puzzle of the sign of the roads variable disappears entirely, since in the alternative specification the logarithm of total road kilometers is always positive and statistically significant. Again, the coefficients of the other conditioning variables and the rates of convergence are essentially unchanged in this new specification. The coefficients of the state dummies, too, are mostly unaffected by the change. Three states do stand out, however. The coefficient for Rajasthan, by far the most sparsely populated state, is considerably reduced in magnitude, and is no longer consistently statistically significant. The coefficient for Kerala, the most densely populated state, also reduces in magnitude and in statistical significance. For West Bengal (also with a high population density), the coefficient actually switches in sign, and in the specification with a single financial development variable, it is now marginally statistically significant. These observations suggest that the relationship between road density and population density bears further investigation. It should also be borne in mind that some of the districts in the sample are heavily urban, which can also have implications for the measured relationship between road kilometers and economic activity and growth. This is also a subject for further investigation. One aspect of the impact of financial depth or financial access on growth is the presence of large outliers in the data, namely cities which are financial centers. Table 16 presents the mean and the ten highest values for the credit-DDP ratio. These outliers may also be biased measures, because credit is obtained through corporate headquarters based in major cities, and counted there in the data, while investments are made in wider geographic areas. In that case, the impact of the credit-DDP variable might be understated in the previous estimates. On the other hand, if these outliers represent a true, strong effect of credit on local growth, then the strong positive coefficient of credit may be driven by these few observations, and therefore higher than if the outliers are omitted. We examine the robustness of the previous results by omitting the seven most extreme outliers as measured by the credit-DDP ratio.
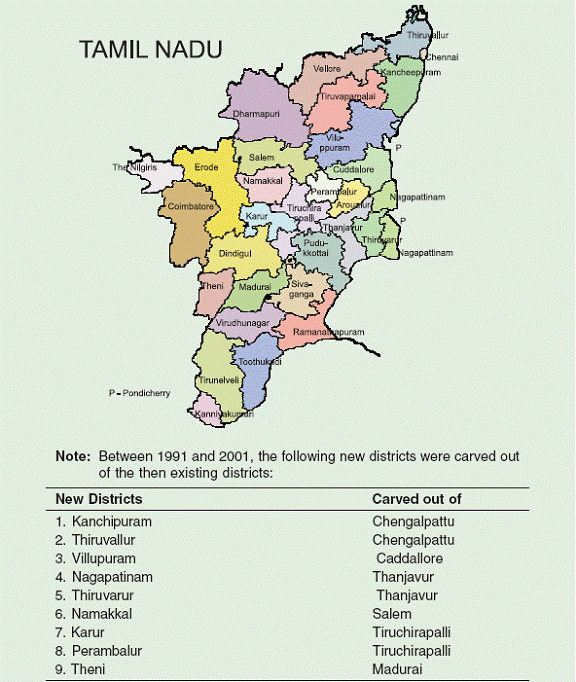
The results for regressions omitting the credit outliers are presented in Table 17, for the standard GLS estimation method.19 We estimate the conditional convergence regression using the two alternative specifications of the credit and deposit variables. Comparing Table 17 with Table 12, we note that the credit and deposit coefficients, or the ratio in the alternative specification, are all somewhat higher in magnitude when the outliers are omitted. However, the statistical significance of the coefficients tends to go down. The latter effect suggests that the outliers indeed were driving some of the earlier results. However, the signs and magnitudes of the coefficients in Table 15 suggest that the credit effect is present, even when the outliers are omitted. Importantly, all the other coefficients are extremely stable, in the sense that they are little changed by omitting the outliers. This supports the robustness of the earlier results with respect to convergence and the impact of human capital in particular on growth. We also examine the robustness of the results to restricting the sample to the four southern states: Andhra Pradesh, Kerala, Karnataka and Tamil Nadu. These results are presented in Table 18. The convergence coefficients are smaller for this subsample, but are significantly different from zero. In the first specification, the roads variable is negative and significant, but that result is not robust to changing the specification of the financial variables. For the southern states, the literacy rate no longer matters in affecting convergence: this result is consistent with the higher and more even literacy rates in the southern states. Most importantly, the financial variables have the right signs in general, and are significant, indicating that financial access matters for growth. This conclusion is tempered slightly by the results in the last column of Table 18, where state dummies are added to the specification of column (1). Andhra Pradesh is the state with an excluded dummy, and therefore the benchmark. The financial variables have the correct signs, but are no longer significant. The dummy coefficients for Karnataka and Tamil Nadu are significant, indicating faster average growth in those states’ districts. Next, we explore the possibility that there are interactions among the conditioning variables. For example, there might be complementarities between access to credit and human capital, in positively affecting growth. In addition, there may be interactions between the conditioning variables and initial per capita DDP, in which case the speed of convergence will depend on the combination of initial conditions. These results are presented in Table 19, again for cluster estimates as well as an iterated GLS method which is similar to maximum likelihood estimation.20 We restrict attention to the specification that uses the credit-deposit ratio, as a measure of financial resource access. The results for the two estimation methods are qualitatively similar, though there are differences in magnitudes, and marginal differences in significance levels. Only the roads variable is robust to this change in specification, remaining positive and significant. The literacy and financial variables now both have negative signs. Furthermore, the interaction terms between the credit-deposit ratio and the roads and literacy measures are negative, though only significant in the iterated GLS estimation. The interpretation of these effects would be as follows. For example, given a particular level of road kilometers, an increase in the credit-deposit ratio has no significant direct effect, but reduces the positive impact of the roads measure on the growth rate. However, interpretation is complicated by the other interaction terms. Thus, the interaction between the credit-deposit ratio and initial per capita DDP is positive (though not statistically significant), implying an increase in the growth rate (and lower speed of convergence). In fact, the interaction of the roads variable with initial per capita DDP is negative and significant. Thus, the results seems to suggest that roads play an important role in increasing growth, and more so for initially poorer districts. Thus, the results in Table 19 tend to favor the importance of roads in equitable development. One potential problem with the specification in Table 19 is that the interaction terms may make it difficult to isolate the impacts of the conditioning variables. An alternative specification allows for interactions, but of the state dummies with initial DDP per capita. Thus, rather than allowing base growth rates (the constant terms) to differ across states, as in Table 15, this specification admits the possibility that convergence rates differ across the states, beyond what is captured by differences in the infrastructure or access variables. The specification is therefore similar to that of Table 11, but with the inclusion of the conditioning variables. These results are presented in Table 20. Again, Andhra Pradesh serves as the benchmark state. Now all three conditioning variables are significant, with the expected positive signs. The interaction terms indicated that convergence was significantly slower than the benchmark state for Karnataka and for West Bengal, and faster for Maharashtra and Uttar Pradesh. These comparative rates of conditional convergence are thus somewhat different than the comparative rates of absolute convergence reported in Table 11. The district level results presented so far use different data than the region-level analysis of the previous section. Hence, we also provide some analysis using data on the variables from region-level analysis, disaggregated to the district level.21 This results in some reduction in sample size, due to missing observations. Table 21 presents results for DDP per capita growth convergence regressions, with the addition of initial year petrol consumption and cereal production per capita as conditioning variables. The results are somewhat hard to interpret, in that the new variables have negative signs, suggesting that districts that were doing well in the base year, as measured by these two economic indicators, have grown more slowly over the subsequent decade. However, the results for the financial variables and for literacy rates are quite robust to the new specification. The results are also not very inconsistent with those in Table 5 of the previous section, with the exception of the sign of the coefficient of base-year petrol consumption. Table 22 provides district level regressions for petrol growth and cereal growth, paralleling the region-level regressions of the previous section. At the district level, we are able to include the measures of human and physical capital that were not available at the region level. The results suggest conditional convergence, and the estimated impacts of literacy and road density are roughly in keeping with the regressions for DDP per capita growth that have formed the main focus of this section. In particular, the financial variables’ estimated impacts seem to be quite robust compared to the DDP growth regressions, especially with the specification using the credit-deposit ratio. Table 23 repeats the specifications of Table 22, but with state dummies included. The effect of this inclusion is somewhat similar to that in Table 21, in which adding the state dummies reduced the significance of the conditioning variables. The result of adding state dummies in Tables 21- 23 is thus somewhat different than was obtained in the base specifications of Tables 13 and 15, where the state dummies did not affect the significance of the conditioning variables. Since the effect of state dummies is greatest in the case of Table 23, this tampering of conclusions with respect to the conditioning variables applies chiefly to the growth of petrol and cereal consumption, rather than to overall growth as measured by DDP per capita. Finally, in Table 24 we present the ten worst districts across the entire data set, based on the most negative residuals. Thus, these represent the districts that are furthest below the regression line, and are therefore districts which performed worse than would have been predicted based on the initial conditions incorporated in the regression. We present results from several alternative specifications in order to provide a sense of the robustness of the results. Variations in the lists indicate that different combinations of initial conditions may be more important in different districts. The results do not necessarily dictate policy responses, but are suggestive of where particular policy attention might be focused, if the objective is to make growth inclusive. Note that the first and fourth set of results for worst districts include state dummies in the specifications. Hence, poor performance relative to the regression line in these cases is relative to the average for that state. In the other two sets of results, poor performance is relative to the overall sample, but still controlling for initial conditions. With the exception of some of the extreme cases, the ranking of the districts appears to be quite sensitive to the particular specification chosen. However, the signs of the residuals are mostly unaffected by the choice of specification. The poor performance of Uttar Pradesh shows up in Table 24, since many of the districts in each set of results are from that state. Of course, the state provides a significant fraction of the sample, but it is noteworthy that districts from Punjab, Tamil Nadu, and West Bengal are not featured in any of the four lists. The results for UP partly reflect the districtlevel data, which seem to indicate overall poor performance of the state, but note that the predominance of the state is robust to the inclusion of state dummies. Examining the geographic distribution of the districts in the four lists (see Appendix 1: District Maps), there is no clear pattern, with the exception of UP. The districts identified as worst performers in this manner are concentrated in the eastern part of the state, which is known to be significantly poorer than the west. Unfortunately, we do not have data for Bihar in our sample, otherwise one might be able to clearly identify a region of worst performance, even after controlling for economic initial conditions.22
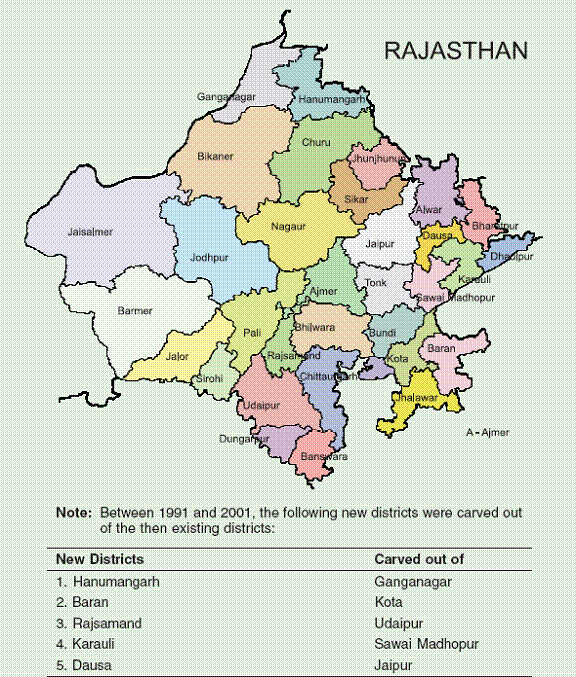
To summarize, the implication of the residuals analysis is that the districts thus identified are doing worse or better than the average, conditional on observable variables included in the regressions. The reasons for deviation from the regression line may be random factors, or unobserved characteristics of those districts, including endogenous policy decisions. Hence, the residual analysis creates guidelines for further investigation of the causes of economic performance, on a case-by-case basis, or possibly for a focused regional strategy (for example, for the eastern Gangetic plain). This section has presented a wide variety of specifications, all involving pooling of district level data. In closing it is useful to summarize what seem to be the main lessons. First, the district-level data for the states in our sample indicates evidence of conditional convergence. This is true across a variety of specifications, including ones without state-level dummies. Hence, the conditional convergence is across the states in the sample, and not just within states. At the same time, there is no evidence for absolute convergence. This result is important, because it suggests that there are identifiable initial conditions that can be affected by policy, and which influence the rate of growth. Hence, targeting these initial conditions provides a basis for policy that leads to more inclusive growth. The most important and robust conditioning variable appears to be the credit-deposit ratio, as a measure of financial access and/or development. Good access to finance appears to be favorable to growth. Second, the literacy rate as a measure of basic human capital, also appears to have an important positive impact on subsequent growth, though this result is somewhat less robust to alternative specifications. Finally, road density as a measure of market access or physical infrastructure in general appears not to have a positive impact on subsequent growth. However, specifications with total road kilometers indicate that access as measured by that variable is a significant positive determinant of future growth. None of these results is surprising, but the empirical analysis presented here allows for an estimation of quantitative impacts, as well as identification of districts where the growth performance lags beyond what is explainable by the conditioning variables used. As noted, our choice was limited by data availability, but the analysis suggests a two-pronged approach, based on first addressing straightforwardly observable growth determinants such as access to credit, education and markets, and, secondly, looking for special factors in particular districts or regions. These factors may include social structures, governance or agro climatic conditions. 9. District Level Analysis: Individual States In this section, we present results for the individual states. In some cases, the number of observations is quite small (as few as 12 for Punjab, for example). Furthermore, intra-state variation in the dependent and independent variables is much less in some cases than inter-state variation. Hence, the results for individual states are less strong, and the regressions are estimated less precisely. However, the differences across states are revealing, in that we impose no restrictions on equality of coefficients across the states. We first present results for each individual state, and then summarize some cross-state comparisons. Since the cluster and GLS techniques used for the pooled regressions are no longer relevant, we present only linear regression results, and we focus on the more parsimonious specification for the credit and deposit variables, using their ratio. However, standard errors are calculated to be robust to intra-state heteroskedasticity in the error terms. Note that, from a national perspective, even each state’s absolute convergence regression can be interpreted as examining convergence conditional on the district being in that state, thereby reflecting state-specific factors that may not be directly measurable. Andhra Pradesh Absolute and conditional convergence regressions for Andhra Pradesh are presented in Table 25. The explanatory power of the overall regressions is fairly low, and individual coefficients are never statistically significant. Hence, there is not too much one can say, except that Andhra Pradesh’s intra-state growth pattern is not well-explained by the regression method used here. One can also assert that there is no obvious evidence for convergence or divergence within the state: although the estimated convergence coefficient is negative and quite large in magnitude, it is not estimated very precisely, and the confidence interval is quite wide. This is somewhat less true of the absolute convergence regression, and since the conditioning variables are insignificant, one may take the absolute convergence estimates as the best explanatory relationship given the data we have.
Karnataka Absolute and conditional convergence regressions for Karnataka are presented in Table 26. The results have some interesting features not present at all in those for Andhra Pradesh, or the pooled regressions. In particular, the roads variable has the expected sign, and is significant at the 5 percent level. The conditional convergence coefficient is negative and very large in magnitude, and it is significant at the 10 percent level.
The absolute convergence coefficient is significant at the 5 percent level, but somewhat smaller in magnitude. This ranking of magnitudes of the two convergence coefficients is typical, though one might expect the standard error in the conditional convergence regression to be somewhat smaller. It is possible that eliminating the two insignificant conditioning variables, might yield the most effective specification of the intra-state growth comparisons. Kerala The results for Kerala are presented in Table 27. The sample size is now quite small, since Kerala has relatively few districts. The absolute convergence regression is a particularly poor fit. In the conditional convergence regression, the variables capturing infrastructure, human development or initial income are insignificant, but the credit variable is highly statistically significant in both specifications. In this case, there is no evidence for intra-state convergence or divergence, as opposed to the weak result in support of convergence for Andhra Pradesh, and stronger result for Karnataka.
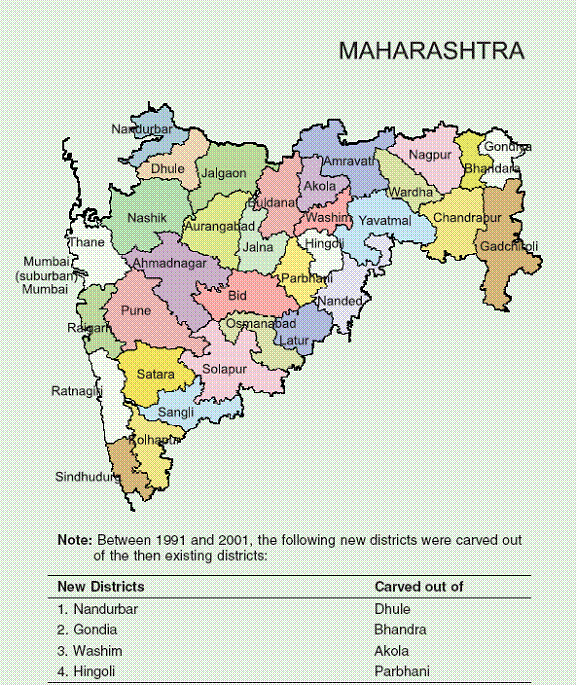
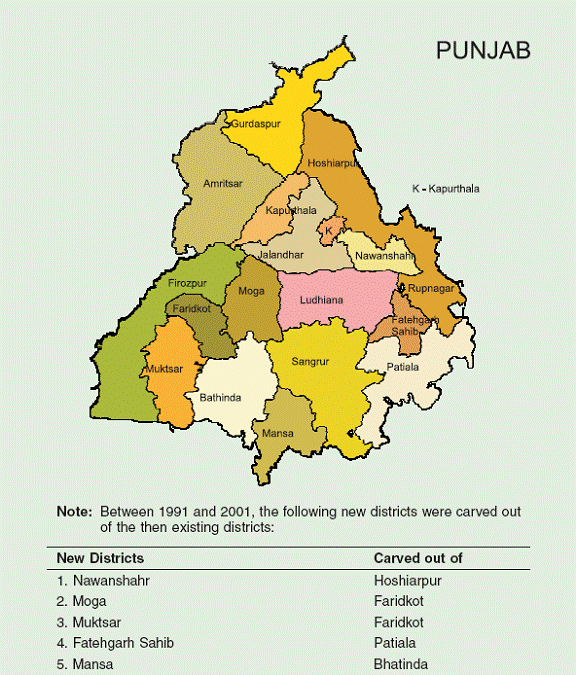
Maharashtra The results for Maharashtra are presented in Table 28. There are two striking features of the regressions. First, the convergence coefficient is extremely high in magnitude, and negative, indicating rapid convergence within the state. Second, the literacy variable is positive and highly significant in the conditional convergence regressions. The roads variable has the right sign, though it is statistically insignificant, while the financial variable is significant at the 10 percent level, with the correct sign. Inclusion of the conditioning variables improves the significance of the convergence coefficient, in contrast to the previous three states. The overall explanatory power of the regression is quite high. Given the presence in Maharashtra of rich urban areas as well as very poor districts in the eastern part of the state, the convergence results are quite striking and bear further investigation. Punjab Results for Punjab are presented in Table 29. Like Maharashtra, Punjab displays high levels of convergence. This is less surprising in the case of Punjab, because it is a smaller state, more homogeneous to begin with. Much of the state is rural, but with a relatively even distribution of mid-sized towns and economic activity. Even though the number of observations is small, the explanatory power of the regressions is quite high. The conditioning variables all have the right signs, though only literacy is significant, and only at the 10 percent level. Since the conditional convergence coefficient is quite similar in magnitude to the absolute convergence coefficient, one could argue that the absolute convergence regression may be the best descriptor of the growth pattern within Punjab given the data we have.
Rajasthan The results for Rajasthan are presented in Table 30. They indicate strong evidence for rapid absolute and conditional convergence within the state, though the coefficients are not as large in magnitude as for Maharashtra and Punjab. Given Rajasthan’s size and sparse population in its desert areas, and its relative poverty, the convergence results are quite striking. In the conditional convergence regression, all the conditioning variables have the correct signs. The physical infrastructure is somewhat close to being significant, while the human development indicator is significant at the 10 percent level. This latter result may be quite relevant for this state, given its tourism-based economy.
Tamil Nadu Results for Tamil Nadu are presented in Table 31. Both the absolute and conditional convergence regressions suggest that there may be some marginal divergence across districts in the state, though the coefficients are not statistically significant. Clearly, though, the growth pattern across districts is very different from the preceding three states’ results summarized above. In fact, none of the coefficients in the conditional convergence regressions are significant, and the overall explanatory power is low. It is worth noting that the four southern states, when examined individually, display quite different patterns of convergence. This observation may be contrasted with the pooled regression for these states, presented in Table 16 in the previous section. One could argue that the pooled regression is misspecified, since it imposes uniformity that is not justified. At the same time, one can argue that there is a regional economy, particularly for Kerala, Tamil Nadu and the southern part of Karnataka, which is better captured with a pooled regression. Clearly there is scope for further investigation of regional patterns of growth.
Uttar Pradesh The results for Uttar Pradesh are presented in Table 32. Perhaps surprisingly, given the size, heterogeneity and relatively poor performance of the state, there is some evidence for intra-state absolute as well as conditional convergence. The coefficients are not large in magnitude, but the conditional convergence coefficient is significant at the 10 percent level. There is also strong evidence that literacy is an important conditioning variable, while credit access has the expected sign, though it is not signficant. One can conjecture that the literacy variable is more significant in states such as Uttar Pradesh, precisely because there is considerable intra-state variation in literacy, as opposed to the southern states.
West Bengal Results for West Bengal are presented in Table 33. The absolute convergence regression is an extremely poor fit, but the conditional convergence regression dramatically improves the explanatory power. All of this improvement is due to the inclusion of the roads variable, which is significant at the 1 percent level in the conditional convergence specification. The conditional convergence coefficient is also significant at the 1 percent level, and is reasonable in magnitude. The other two conditioning variables have no explanatory power at all.
Cross-state comparisons A summary of the results for the nine states in the sample is provided in Tables 34 and 35. Table 34 also compares the individual state absolute convergence regressions with the pooled regression from Table 11. Note that the pooled regression uses dummies and interaction terms to allow the base growth rates and convergence coefficients to differ across states. Therefore the difference in the two sets of results can be attributed to differences in assumptions about error terms. The results are qualitatively quite similar, indicating that the pooled regression, imposing some homogeneity of error structure, but allowing the coefficients to be different across states, may be reasonable for the absolute convergence case.
In Table 35, based on the conditional convergence regressions, a ‘yes’ indicates significance at the 10 percent level or better. Blanks indicate no significant relationship for either specification. Two southern states in the sample, Andhra Pradesh and Tamil Nadu, are similar in that there are no statistically significant effects in the convergence regressions, and no significant evidence of convergence or divergence. Kerala is similar in the latter result, but the credit measure is significant for Kerala. In the case of Karnataka, there is evidence of convergence, as well as the importance of road infrastructure. Of the other five states, the northern states of Punjab, Rajasthan and Uttar Pradesh do share boundaries, but are quite different in their economies and geography. Nevertheless, they all have similar results in that they display strong evidence for conditional convergence. In all three of these states literacy is a significant conditioning variable. Maharashtra, the sole state in the west (though it shares a significant border with Karnataka), has the strongest evidence of conditional convergence, and both literacy and credit are positive and significant. In the case of West Bengal, the sole eastern state, the measure of physical infrastructure or market access, namely the density of road kilometers, is statistically significant, with the correct positive sign. For Rajasthan and Uttar Pradesh, the results on literacy could be of particular interest, because both these states have been relatively poor. While the individual state regressions say nothing about relative state performance, they do suggest that income levels within the states are converging, i.e., poorer districts may be catching up. The results are also of interest for these two cases because both states are large, and have considerable intra-state diversity. The results suggest that it is not the case that certain regions in each state are growing faster than others, widening within-state inequality. This is also true for Maharashtra, which is much richer, but also very diverse, with a much poorer hinterland along with affluent western cities. In Table 36, we summarize the best and worst districts for each state, in terms of residuals from the individual state absolute convergence regressions. Thus, a district with a large negative residual has done worse than the average, given its initial income levels, while a district with a large positive residual has done better than average, conditional on initial per capita income. As one might expect, many of the worst performing districts by this criterion lie in interior or remote regions, though this pattern is less relevant or applicable for states such as Kerala and Punjab. Districts that are centers of commercial activity, with thriving towns or cities, seem to do better than average, again as one would expect. Recent economic policy in India has emphasized the idea of inclusive growth. In some ways, this is a return to the pre-liberalization conceptual framework, in that equity across the country and reduction of rural poverty have been receiving greater attention. Of course there has always been a governmental apparatus for addressing these issues, but they became more pressing with market-oriented economic reforms seeming to exacerbate inequalities, including regional inequalities. Much of the evidence for these trends came from very micro studies, or alternatively from comparisons across states through growth regressions. While the states are important political and policy-making entities, they are also large enough that focusing on state-level trends can miss out on more localized problems of relative or even absolute economic stagnation. This is where our study seeks to fill a gap. Examining growth at the levels of NSSO regions and districts allows one to identify more closely the areas of good and poor performance within India. While we do not have data for all districts, the coverage is quite good, in that it includes a wide cross-section of states. There are two sorts of policy implications that can be drawn from the analysis. The first looks at the regression coefficients, and derives policy recommendations from the estimated average behavior. Thus, the district level convergence regressions are supportive of the view that improving literacy rates and road connectivity can be important factors in accelerating local growth. Similarly, there is evidence that credit access can have a positive impact on growth. The second policy implication comes from identifying districts that are well below the estimated average relationships between growth and initial conditions. These districts may be suffering from other deficits, or particular obstructions that can potentially be identified and focused on through appropriate policy measures. Thus, the analysis allows an identification of different sets of policy recommendations for different situations at the district level. The value of our study for policy-makers is therefore in (1) identifying types of investment that may improve the growth prospects of lagging regions or districts, allowing better targeting by national and state-level policy makers; and (2) identifying specific districts or regions where economic performance is not fully or well explained by the initial conditions measured here, thereby suggesting where additional data collection and analysis may be beneficial. We must also make clear the limitations of this study for policymaking. First, the set of variables used is not comprehensive, and additional broad data collection may lead to a more encompassing set of conditioning variables, which could change the policy conclusions. Social fragmentation, land systems and governance quality are all examples of factors that are likely to be important as growth determinants. Second, the analysis provides no guidance on the specific design of policies, or of institutions for policy implementation. Much of the criticism of Indian policies with respect to promoting inclusive growth has focused on issues of detailed policy design, and effectiveness of implementation. Our analysis cannot provide any lessons on how to improve literacy or improve access to credit: it merely confirms that these issues are important for understanding growth performance at a fine-grained level. This study represents the first detailed growth analysis of Indian data below the state level. Since states in India are very large and heterogeneous, cross-state comparisons and growth regressions, of which there are many, can be of limited usefulness. This study extends previous growth analysis by examining the growth mechanisms within India at the district level, allowing a more refined understanding of India’s regional disparities, and possible appropriate policy responses. The study provides evidence that access to credit, literacy and access to roads all matter to some degree for growth, even when one examines growth performance at the district level. In many ways, the district is the most significant economic and administrative unit in the country, and mapping growth performance and determinants as we have done provides additional guidance for policy makers in terms of where to focus policy attention. However, this empirical analysis cannot provide lessons on detailed policy design or implementation strategies. Clearly, the study is also limited by the availability and quality of the data. Perhaps the most immediate lesson of the study is in pointing out the need for further and better data collection and for more detailed empirical analysis. Arguably, the success of India’s push for inclusive growth will depend partly on better understanding of the factors that will make broad based growth more likely, and this study can be seen as an initial contribution to this effort. Abramovitz, Moses (1986): ‘Catching up, Forging Ahead and Falling Behind, Journal of Economic History, Vol 46, June, pp 385-406. Adabar, K. (2005): The Regional Dimensions of Economic Growth in India’s Federalism, PhD dissertation, Institute for Social and Economic Change, Bangalore. Ahluwalia, Montek S. (2000), Economic Performance of States in Post- Reforms Period, Economic and Political Weekly, May 6, 1637-48. Ahluwalia, Montek S. (2002), ‘State Level Performance Under Economic Reforms In India,’ in Anne Krueger, ed., Economic Policy Reforms and the Indian Economy, Chicago: University of Chicago Press Aiyar, Shekhar (2001), ‘Growth Theory and Convergence across Indian States: A Panel Study’, in Callen, Tim, Patricia Reynolds, and Christopher Towe (eds.). India at the Crossroads: Sustaining Growth and Reducing Poverty, International Monetary Fund, Washington DC. Alesina, A and R Perotti (1993): ‘Income Distribution, Political Instability and Investment’, NBER Working Paper, No 4486, National Bureau of Economic Research, Cambridge Ma. Annigeri, V. B. (2003), ‘‘District Health Accounts: An Empirical Investigation’’, Economic and Political Weekly, May 17, 1989-1993. Anselin, L. (1995). ‘Local Indicators of Spatial Association—LISA,’ Geographical Analysis 27, 93-115. Bajpai Nirupam and Jeffrey Sachs (1999), “The Progress of Policy Reform and Variations in Performance at the Sub-National Level in India”, Development Discussion Paper No. 730, Harvard Institute for International Development, November. Rao, M. Govinda and Kunal Sen (1997), Internal Migration, Centre-State Grants, and Economic Growth in the State of India: A Comment on Cashin and Sahay, International Monetary Fund Staff Papers, 44, 2, 283-88. Barro, Robert (1991): Economic Growth in a Cross-Section of Countries, Quarterly Journal of Economics, 106, No 2, May, 407-43. Barro, Robert and Xavier Sala-i-Martin (1991): Convergence across States and Regions, Brookings Papers on Economic Activity, I, pp 107-81. Barro, Robert and Xavier Sala-i-Martin (1992), “Convergence”, Journal of Political Economy, 100, 223-51. Barro, Robert and Xavier Sala-i-Martin (1995): Economic Growth, McGraw- Hill, New York Bhalla, Surjit S (2000): ‘Growth and Poverty in India – Myth or Reality’, paper prepared for a Conference in Honour of Raja Chelliah, Institute of Economic and Social Change, Bangalore, January 17. Bhalla, Surjit S. (2002), Imagine There is No Country: Poverty, Inequality and Growth in the Era ;of Globalization, monograph, Oxus Research, www.oxusreasearch.com/downloads/Imag.June2002a.pdf. Bhandari, Laveesh and Aarti Khare (2002), ‘The Geography of Post 1991 Indian Economy,’ Global Business Review, Vol. 3, No. 2, 321-340. Bharadwaj, Krishna (1982): Regional Differentiation in India A Note, Economic and Political Weekly, Annual Number, April. Bils, Mark and P Klenow (1996): ‘Does Schooling Cause Growth?’ American Economic Review, Vol 90, No 5, pp 1160-83 Boadway, Robin and Frank Flatters (1982): Equalisation in a Federal State: An Economic Analysis, Economic Council of Canada. Boadway, R, I Horiba and R Jha (1999): ‘The Provision of Public Services by Government Funded Decentralised Agencies’, Public Choice, vol 100, no 3 and 4, pp 157-84. Borts, G.H. (1960), ‘‘Regional Cycles of Manufacturing Employment in the US, 1914-1953’, Journal of the American Statistical Association 55, 151-211. Boyle, G and T McCarthy (1997): ‘A Simple Measure of ß Convergence’, Oxford Bulletin of Economics and Statistics, vol 59, no 2, pp 257-64. Bramall, Chris, and Jones, Marion (1993): ‘Rural Income Inequality in China since 1978’, Journal of Peasant Studies, 21(1). Breton, Albert (1996): Competitive Governments, Cambridge University Press, Cambridge. Bruno, M, M Ravallion and L Squire (1996): ‘Equity and Growth in Developing Countries: Old and New Perspectives on the Policy Issues’, Policy Research Working Paper, 1563, World Bank. Calzonetti, F.J. and R.T. Walker (1991),’‘Factors Affecting Industrial Location Decisions: A Survey Approach’’, in H.W. Herzog and A.M. Schlottmann (ed.) Industry Location and Public Policy, The University of Tennessee Press: Knoxville. Cashin, P. and R. Sahay, 1996, “Internal Migration, Centre-State Grants and Economic Growth in the States of India”, IMF Staff Papers, Vol. 43. 1, 123-171. Cass, David (1965): Optimum Growth in an Aggregative Model of Capital Accumulation, Review of Economic Studies, Vol 32, July, pp 233-40. Chakravorty, S. (2000), ‘‘How Does Structural Reform Affect Regional Development? Resolving Contradictory Theory with Evidence from India’’, Economic Geography, 76, 367-94. Chakravorty, S. (2003), ‘‘Capital Source and the Location of Industrial Investment: A Tale of Divergence from Post-Reform India’’, Journal of International Development, 15, 365-83. Chapman, K. and D.F. Walker (1991), Industrial Location: Principles and Policies, Basil Blackwell: Oxford. Chinitz, B. (1961), ’‘Contrasts in Agglomeration: New York and Pittsburgh’’, American Economic Review, 51, 279-89. Choudhury, Uma Datta Roy (1993): Interstate and Intra-State Variations in Economic Development and Standard of Living, National Institute of Public Finance and Policy, New Delhi. Ciccone, A. and R. Hall (1996), ‘‘Productivity and the Density of Eeconomic Activity’’, American Economic Review, 86, 54-70. Das, S K and Alokesh Barua (1996): Regional Inequalities, Economic Growth and Liberalisation: A Study of the Indian Economy, The Journal of Development Studies, Vol 32, No, February, pp 364-90. Dasgupta, D., P. Maiti, R. Mukherjee, S. Sarkar and S. Chakrabarti (2000), ‘‘Growth and Interstate Disparities in India’’, Economic and Political Weekly, July 1, 2413-22. Datt, Gaurav (1997): Poverty in India and Indian States: An Update, International Food Policy Research Institute, Washington, DC. Datt, Gaurav (1999): ‘Has Poverty Declined Since Economic Reforms?’ Economic and Political Weekly, Vol 34, No 50. Datt, G and M Ravallion (1998): ‘Why Have Some Indian States Done Better than Others at Reducing Rural Poverty?’, Economica, vol 65, no 1, pp 17-38. Deaton, Angus and Jean Dreze (2002), “Poverty and Inequality in India: A Re-Examination”, Economic and Political Weekly, September 7, 3729-3748. Debroy, B. and L. Bhandari (2003), District-Level Deprivation in the New Millennium, Konark Publishers Pvt Ltd, Delhi. Deininger, K and L Squire (1997): ‘Economic Growth and Income Inequality: Reexamining the Links’, Finance and Development, March. Dholakia, Ravindra H (1977): ‘State Income Inequalities in India and Interstate Variations in Price Movements’, presented at the conference of Indian Association for Research in National Income and Wealth (IARNIW) held at Shillong in November. Subsequently it was published in Arthavikas Vol 14, No 1, January 1978. – (1985): Regional Disparity in Economic Growth in India, Himalaya Publishing House, Bombay. Dholakia, R. (1994), ‘‘Spatial Dimension of Acceleration of Economic Growth in India’’, Economic and Political Weekly, August 21, 29 (35), 2303-09. Dholakia, R. (2003), ‘‘Regional Disparity in Economic and Human Development in India’’, Economic and Political Weekly, September 27. Dholakia, Bakul H and Ravindra H Dholakia (1980): ‘State Income Inequalities and Interstate Variation in growth of Real Capital Stock’, Economic andPolitical Weekly, Vol XV, No 38, September 20, pp 1586-591. Dhongde, S. (2004), ‘‘Decomposing Spatial Differences in Poverty in India’’, WIDER Research Paper No. 2004/53, August, United Nations University. Dreze, Jean and Amartya Sen (2002), India: Development and Participation,New Delhi: Oxford University Press. EPW Research Foundation (1994): ‘Social Indicators of Development for India – II: Interstate Disparities’, Economic and Political Weekly, Vol XXIX, No 21, May 21, (Special Statistics – 8) Evans, P and G Karras (1996): Do Economies Converge? Evidence from a Panel of US States, Review of Economics and Statistics, Vol 78, August, pp 384-88. Evans, P and G Karras (1996): ‘Convergence Revisited’, Journal of Monetary Economics, vol 37, no 2, pp 249-65. Evenett, S.J. and W. Keller (2002), ‘‘On Theories Explaining the Success of the Gravity Equation’’, Journal of Political Economy, 110, 281-316. Feser, E.J. and E.M. Bergman (2000), ‘‘National Industry Cluster Templates: A Framework for Applied Regional Cluster Analysis’’, Regional Studies, 34, 1-20. Fishlow, A (1995): ‘Inequality, Poverty and Growth: Where Do We Stand?’, Annual Conference on Development Economics, World Bank. Franciso, F, G Prennushi and M Ravallion (1999): ‘Protecting the Poor from Macroeconomic Shocks: An Agenda for Action in a Crisis and Beyond’, mimeo, The World Bank. Friedman, J. (1973), ‘‘A Theory of Polarized Development’’, in J. Friedman (ed) Urbanization, Planning and National Development, Sage: Beverly Hills. Fujita, M., P. Krugman and A. Venables (1999). The Spatial Economy: Cities, Regions, and International Trade, MIT Press: Cambridge MA. Fujita, M. and J.F. Thisse (1996). ‘Economics of Agglomeration’, Center for Economic Policy Research Discussion Paper 1344. Gaiha, R and V Kulkarni (1999): ‘Is Growth Central to Poverty Alleviation in India?’ Journal of International Affairs, vol 52, no 1, pp 145-80. Galor, O (1996): Convergence? Inferences from Theoretical Models, The Economic Journal, Vol 106, pp 1056-69. Geeta Rani, P (1995): ‘Human Development index in India: A District Profile’, Arthavijnana, Vol XLI, No 1, March pp 09-30. Ghosh, B., S. Marjit and C. Neogi (1998), ‘‘Economic Growth and Regional Divergence in India, 1960 to 1995’’, Economic and Political Weekly, June 27 – July 3, 33 (26), 1623-30. Ghosh, B. and P. De (1998): ‘Role of Infrastructure in Regional development: A Study of India over the Plan Period,’ Economic and Political Weekly, Vol. 33, No. 47 and 48, 3039-48. Gopalan, C (1985): ‘The Mother and Child in India’, Economic and Political Weekly, Vol XX, No 4, January 26, pp 159-66. Government of Kerala (2002): ‘Modernising Government Programme (MGP)’, web site: http://www.keralagov.com Griffin, K, and Zhao Renwei (eds) (1993): The Distribution of Income in China, Macmillan, London. Guilmoto, C. Z. and S. I. Rajan (2002), ‘‘District Level Estimates of Fertility from India’s 2001 Census’’, February 16, 665-672. Gupta, S (1995): ‘Economic Reform and Its Impact on the Poor’, Economic and Political Weekly, June, pp 1295-1313. Gylfason, Thorvaldur (1999): Principles of Economic Growth, Oxford University Press, Oxford. Hansen, W.G. (1959). ‘How Accessibility Shapes Land Use’, Journal of American Institute of Planners 25:73-6. Hanushek, E.A. and B.N. Song (1978). ‘The Dynamics of Postwar Industrial Location’, The Review of Economics and Statistics 60:515-22. Harrington, J.W. and B. Warf (1995). Industrial Location: Principles, Practice, and Policy, Routledge: London and New York. Henderson, V. (1988). Urban Development: Theory, Fact, and Illusion, Oxford University Press: New York. Henderson, V. (2000). ‘The Effects of Urban Concentration of Economic Growth’, NBER Working Paper 7503, National Bureau of Economic Research: Cambridge MA. Hirschman, A.O. (958) The Strategy of Economic Development, Yale University Press: New Haven. Indira, A., M. Rajeev and V. Vyasulu (2002), ‘‘Estimation of District Income and Poverty in Indian States’’, Economic and Political Weekly, June 1, 2171-2177. Jacobs, J. (1969). The Economy of Cities, Vintage: New York. Jeromi, P D (2003): ‘What Ails Kerala’s Economy: A Sectoral Exploration’, Economic and Political Weekly, Vol XXXVIII, No 16, April 19-25, pp 1584- 1600. Jha, R. (2000), ‘‘Growth, Inequality and Poverty in India – Spatial and Temporal Characteristics’’, Economic and Political Weekly, March 11, 921- 928. Jha, R, M Mohanty, S Chatterjee and P Chitkara (1999): ‘Tax Efficiency in Selected Indian States’, Empirical Economics, vol 24, no 4, pp 641-54. Kalirajan, K P and Richard T Shand (1996): Inter-Sectoral Linkages in India, PN 9426, Working Paper No 4, ASARC, The Australian National University. Khan, A R and Riskin, C (2001): Inequality and Poverty in China in the Age of Globalisation, Oxford University Press, New York. Krishnaji (1993): ‘Widening Distances: State Domestic Product Variations, 1961-81’ in Pranab Bardhan et al (eds), Development and Change: Essays in Honour of K N Raj, Oxford University Press, Bombay. Krugman, P. (1991). ‘Increasing Returns and Economic Geography’, Journal of Political Economy 99:483-99. Kurian, N J (2000): ‘Widening Regional Disparities in India: Some Indicators’, Economic and Political Weekly, Vol XXXV, No 7, February 12 pp 538-50. Kuznets, Simon (1955): Economic Growth and Income Inequality, American Economic Review, Vo 45, pp 1-28. Lall, S. V. and S. Chakravorty (2004), ‘‘Industrial Location and Spatial Inequality: Theory and Evidence from India’’, WIDER Research Paper No. 2004/49, August, United Nations University. Lall, S.V., R. Funderburg and T. Yepes (2004b). ‘Location, Concentration, and Performance of Economic Activity in Brazil’, World Bank Policy Research Working Paper 3268, World Bank: Washington DC. Lall, S.V., Z. Shalizi, and U. Deichmann (2004a). ‘Agglomeration Economies and Productivity in Indian Industry’, Journal of Development Economics 73:643-73. Lipton, M and M Ravallion (1995): ‘Poverty and Policy’ in J Behrman and T Srinivasan (eds), Handbook of Development Economics, vol III, pp 2551- 2657, Amsterdam: North Holland. Lucas, Robert E, Jr (1988): On the Mechanics of Development Planning, Journal of Monetary Economics, Vol 22, July, pp 3-42. Marjit, S. and S. Mitra, 1996, “Convergence in Regional Growth Rates: Indian Research Agenda”, Economic and Political Weekly, August 17, 31 (33), 2239-42. Markusen, A., P. Hall, S. Campbell, and S. Deitrick (1991). The Rise of the Gunbelt: The Military Remapping of Industrial America, Oxford University Press: New York. McCann, P. (1998). The Economics of Industrial Location: A Logistics- Costs Approach, New York: Springer. Mishra P., and A. Parikh (1997). ‘Distributional Inequality in Indian States’, Journal of Income Distribution 7:89-108. Morris, David and Michelle B McAlpin (1982): Measuring the Condition of India’s Poor, Promilla and Co, New Delhi. Mueller, E. and J.N. Morgan (1962). ‘Location Decisions of Manufacturers’, Papers and Proceedings of the Seventy-Fourth Annual Meeting of the American Economic Association, American Economic Review 52: 204-17. Myrdal, G. (1957). Economic Theory and Underdeveloped Regions, Duckworth: London. Nagaraj, Rayaprolu, Aristomene Varoudakis and Marie-Ange Veganzones (1998), “Long-Run Growth Trends and Convergence across Indian States,” OECD Technical Paper No. 131. Nagaraj, R (2000): ‘Indian Economy since 1980: Virtuous Growth or Polarisation?’, Economic and Political Weekly, August 5. Nagaraj, R., A. Varoudakis, and M. A. Veganzones, 2000, “Long-Run Growth Trends and Convergence across Indian States”, Journal of International Development, Vol. 12. Panikar, PGK (1980): ‘Inter-Regional Variation in Calorie Intake’, Economic and Political Weekly, Vol XV, No 41, 42 and 43, October, pp 1803-14. Persson, T and G Tabellini (1991): ‘Is Inequality Harmful for Growth? Theory and Evidence’, Centre for Economic Policy Research Discussion Paper 581. Planning Commission of India (2002), National Human Development Report, http://planningcommission.nic.in/nhdrep/nhd2001.pdf. Rajan, S.I. and P. Mohanchandran (1998). ‘Infant and Child Mortality Estimates–Part I,’ Economic and Political Weekly, Special Statistics, 9 May, 34:1120-40. Raman, J. (1996), ‘‘Convergence or Uneven Development: A Note on Regional Development in India’’, Valparaiso University, US, mimeographed. Rao, M G (1997): Intergovernmental Fiscal Relations in a Planned Economy The Case of India, paper presented at the Conference on Fiscal Decentralisation in Developing Countries, Montreal, September. Rao, M Govinda, R.T Shand, and K.P.Kalirajan, 1999, “Convergence of Income across Indian States: A Divergent View”, Economic and Political Weekly, March 27-April 2, 34 (13), 769-78. Rao, M.Govinda, and Nirvikar Singh (1998), “Fiscal Overlapping, Concurrency and Competition in Indian Federalism,” CREDPR Working Paper 30b, December. Ravallion, M (1998): ‘Does Aggregation Hide the Harmful Effects of Inequality on Growth?’, Economics Letters, vol 61, no 1, pp 73-77. Rebello, Sergio (1991): Long Run Policy Analysis and Long Run Growth, Journal of Political Economy, Vol 99, No 3, June, pp-21. Reserve Bank of India (2002), Report on Currency and Finance 2000-01, Mumbai. Romer, Paul M (1990): Endogenous Technological Change, Journal of Political Economy, Vol 98, No 5, October, pp S71-S102. Roy Choudhury, Uma Dutta (1993): ‘Interstate and Intrastate Variations in Economic Development and Standard of Living’, Journal of Indian School of Political Economy, Vol V, No 1, January-March, pp 47-116. Sachs, Jeffrey D.,Nirupam Bajpai and Ananthi Ramiah (2002), “Understanding Regional Economic Growth in India,” CID Working Paper No.88, Harvard University, March. Sarkar, P. C. (1994), ‘‘Regional Imbalances in Indian Economy over Plan Periods’’, Economic and Political Weekly, March 12, 29 (2), 621-33. Sastry, N. S. (2003), ‘‘District Level Poverty Estimates – Feasibility of Using NSS Household Consumer Expenditure Survey Data’’, Economic and Political Weekly, January 25, 409-12. Shaw, G K (1992): ‘Policy Implications of Endogenous Growth Theory,’ Economic Journal, May, pp 611-21. Singh, Nirvikar, Laveesh Bhandari, Aoyu Chen and Aarti Khare (2003): ‘Regional Inequality in India: A Fresh Look’, Economic and Political Weekly, Vol XXXVIII, No 11, March 15-21, pp 1069-73. Singh, Nirvikar and T.N.Srinivasan (2005), “Indian Federalism, Globalization and Economic Reform,” in T.N. Srinivasan and Jessica Wallack, eds., Federalism and Economic Reform: International Perspectives, Cambridge, UK : Cambridge University Press, 301-363. Sinha, T. and D. Sinha (2000): ‘No Virginia, States in India are NOT Converging,’ International Indian Economic Association, Working Paper No. 2000-09-01. Solow, Robert (1956): A Contribution to the Theory of Economic Growth, Quarterly Journal of Economics, Vol 70, No 1, February, pp 65-94. Solow, Robert M (1994): ‘Perspectives on Growth Theory, Journal of Economic Perspectives, Winter, pp 45-54 Subrahmanyam, S. (1999), ‘‘Convergence of Income across States’’, Economic and Political Weekly, November 20, 34 (46 & 47), 3327-28. Swan, Trevor W (1956): Economic Growth and Capital Accumulation, Economic Record, Vol 32, November, pp 334-61. UNDP, State Human Development Reports, Human Development Resource Centre, New Delhi. Webber, M.J. (1984). Industrial Location, Sage: Beverly Hills. Williamson, J.G. (1965). ‘Regional Inequality and the Process of National Development’, Economic Development and Cultural Change 13 (1), Part II:3 Yao Shujie (1999): ‘Economic Growth, Income Inequality and Poverty in China under Economic Reforms’, Journal of Development Studies, 35. Zaidi, Naseem A and Md Abdul Salam (1998): ‘Human Development in India; An Interstate Comparison’, Indian Journal of Economics, Vol LXXVIII, No 311, April, pp 447-60. Appendix 1: District Maps of States
* Dr. Nirvikar Singh is a Professor at University of California, Santa Cruz, USA and Mr. Jake Kandall is with the World Bank. Shri R. K. Jain is Director and Dr. Jai Chander is Assistant Adviser in the Department of Economic Analysis and Policy, Reserve Bank of India. 1 The bibliography provides extensive references on neoclassical and endogenous growth theory and empirical applications to convergence issues. 2 Ghosh and De (1998) and several other studies discussed in this section emphasize the role of various aspects of infrastructure in explaining differential growth performances across the states. 3 Marjit and Ghosh (2000) obtain results quite consistent to those of RSK, for the period 1970-96, using a slightly different sample of states and somewhat different data. Interestingly, they exclude most of the special category states ‘endogenously’, based on an outlier analysis. Commenting on Rao et al (1999), Subrahmanyam (1999) has argued for inclusion of capital formation, work participation and technology as factors influencing growth across states. 4 This is true whether one uses a one-sided or two-sided test. 5 See Singh and Srinivasan (2005) for further details. 6 Sinha and Sinha (2000) consider political stability at the state level, rather than size, and find that it has a positive impact on growth. They do not find any evidence of absolute or conditional convergence. 7 See also Shand and Bhide (2000) for further empirical analysis, including sectoral decompositions. Chaudhuri (2000) also profiles Indian states’ growth experience, amplifying the work of Ahluwalia, and highlighting some of the differences between the 1990s and earlier decades. 8 Ahluwalia’s regressions are effectively restricted versions of convergence regressions, with the parameter of initial income level set to zero. 9 To the extent that the HDI better measures what we care about – including material standards of living as one component, in addition to access to basic needs – it could be argued that this tradeoff is tolerable, if not too steep. Note also that Singh et al (2003) find no evidence of divergence in HDI across states, for the 1990s. Choudhury (1993), in an earlier study, also finds that inter-state variations in consumption are less severe than those in income: again consumption may be preferable over income as a short-term measure of welfare. 10 This acronym was coined because of its similarity to the Hindi word bimar, meaning ‘ill.’ There are two points to note. First, the coinage was meant to apply to the undivided states, including, therefore, what are now the new states of Chhattisgarh, Jharkhand and Uttarakhand. Second, it excluded Orissa, which is in many ways in the same category of most backward or poorest states. In any case, the purpose of the current study is to go below these state-level characterizations, because seemingly better-off states such as Maharashtra, Karnataka and Andhra Pradesh may also have portions that are quite backward in terms of human and economic development. 11 Given that Jharkhand was part of the undivided Bihar state (and therefore part of the BIMARU group), this count yields the remarkable fact that over half of the most backward districts of India are in that specific region, once, very long ago, the center of Indian civilization. 12 Missing data for some districts within Uttar Pradesh and West Bengal also slightly reduce the coverage of our sample. 13 To the extent that rural India and poorer regions are lagging in relative shares of the economy, this picture is consistent with increasing regional inequality of economic outcomes. However, this is not a direct inference from the results of Bhandari-Khare, since they are given in terms of changing relative shares, not absolute performance. It should also be noted that agriculture’s growth would in any case be slower in an economy undergoing development and structural change. Finally, the data do not cover the most recent period of rapid growth and the latest policy attempts to boost rural incomes. 14 We are indebted to Laveesh Bhandari and Indicus Analytics for making this data available to us. 15 The original data set that was collected consisted of 215 districts, but after inspection, we omitted five districts where there appeared to be inconsistencies in the data. The regression results are not qualitatively affected by the omission or inclusion of these five districts, but individual residuals for the omitted districts were deemed to be unreliable, favoring exclusion from the analysis. 16 This problem also exists in cross-country convergence regressions, where countries as disparate in size as India and Nepal will each be treated as equally influential observations in a regression. 17 At most, one can include something like zonal dummies (e.g., for north, south, east and west), but unless a panel is used, the degrees of freedom are very limited in state-level regressions. 18 The period is such that Bihar would include Jharkhand and Madhya Pradesh would include Chhattisgarh. 19 The cluster method gives results that are not substantially different, and those are not reported. 20 We also tried iterated GLS for several other specifications reported earlier, and found that the results were qualitatively similar to those from the standard heteroskedasticity-robust estimation, which we have mainly reported. 21 We are grateful to the report referee, Laveesh Bhandari, for suggesting this exercise to link the two levels of analysis, and for providing us with the data. 22 It is also important to note that there is some missing data, even for the states in our sample. In some cases, the data was simply not available, while in a handful of cases, the data did not seem reliable enough to us, and we omitted those districts as a result. Appendix 2 lists all the districts in our sample, and a comparison with the district maps allows determination of which districts are excluded. In particular, all the districts of Uttarakhand, shown in the district map as part of Uttar Pradesh, are excluded from our sample. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Page Last Updated on: