Conventional Value at Risk models are severely constrained while dealing with liquidity risk. This inevitably leads to an underestimation of overall risk and consequently misapplication of capital for the safety of financial institutions. Standard Value at Risk (VaR) model assumes that any quantity of securities can be traded without influencing market prices. In reality, most markets are less than perfectly liquid and many securities cannot be traded with ease in markets. This is especially true for emerging market economies where the process of financial sector reform and deepening is currently taking place. Despite episodic evidences of liquidity crisis in the Indian financial markets, risks associated with market illiquidity have not been effectively incorporated into the VaR models. In the face of sudden and persisting off-market prices of some of the securities in their portfolio, the Indian financial organizations often find it difficult to offload these securities without booking significant trading losses. As a consequence, several securities exhibit very low levels of turnover in the secondary segment of the debt market. Also, in most cases, measures of market risk fail to capture the costs of carrying illiquid assets in their portfolio. This becomes a constraining factor for market growth. In this context, the paper attempts to construct a Liquidity adjusted VaR model (L-VaR model) that incorporates liquidity risk in Value at Risk models. The paper tests the performance of L-VaR model vis-a-vis existing VaR models and finds that in the Indian context, the liquidity risk is an important component of the aggregate risks absorbed by the financial institutions.

JEL Classification : G11, G18.

Keywords : Liquidity Risk, Volatility, Value at Risk, GARCH, Turnover, Liquidity Adjustment Facility.

Liquidity in financial market implies the ability to transact large amount of securities quickly at low cost. Classically allied to the notions of marketability and market depth, the accepted definition of liquidity is in terms of the deviation of the market price from fair value due to trading frictions. This is quantified by, among others,

* Assistant Adviser, Department of Economic Analysis and Policy, Reserve Bank of India. The paper was presented at the Seventh Money and Finance Conference at Indira Gandhi Development Research Institute (IGIDR) in February 2005. I thank Philippe Jorion, Rene Stulz, Dilip Nachane, Vikas Chitre and A. V. Rajwade for their comments on the paper. The views in this paper are those of the author and not necessarily of the institution to which he belongs.

the bid-ask spreads, turnover information and processing costs. According to Black (1971), a market is liquid if, at any time, (a) there is an ‘ask price’ and a ‘bid price’ for an investor who wants to buy or to sell immediately a minimal quantity imposed by the market authorities; (b) the bid-ask spread is always tight; (c) in the absence of a ‘special’ information, an investor who wants to buy or to sell a big quantity can expect a price, on average, close to the current market price; (d) an investor can buy or sell a large ‘block’ immediately by paying a premium (discount) which is positively related to the volume.

BIS (1999) defines asset liquidity according to at least one of three dimensions: depth, tightness and resilience. Tightness, measured by bid-ask spread, indicates how far transaction price diverges from the mid-price. Depth defines the maximum number of shares that can be traded without affecting prevailing quoted market prices. Finally, resilience denotes the speed with which price fluctuations resulting from trades are dissipated or how quickly markets clear order imbalances.

Despite episodic evidences of liquidity crisis in Indian financial markets, risks associated with market illiquidity have not been effectively incorporated into the Value-at-Risk (VaR) models. In the face of sudden and persisting off-market prices of some of the securities in their portfolio, the Indian financial organizations often found it difficult to offload these securities without booking significant trading losses. Moreover, in most cases, risk measures failed to capture the costs of carrying illiquid assets in their portfolio. As a consequence, a whole bunch of securities were not traded by financial firms. This became a constraining factor for market growth. With the gradual move towards marking to market of the portfolio to truly capture the risks of holding the securities, the pricing of untraded illiquid assets posed an additional challenge. For many securities, actual trades were absent on many trading days and it was clear that prices derived from zero coupon yield curve differed significantly from trading prices in reality.

In the Indian debt market, the challenge of incorporating liquidity risk was faced in the measurement of value at risk for Primary Dealers (PDs) in Government Securities. The Value at Risk model was introduced for the PDs as a pioneering approach to effectively assess the market risk of these highly leveraged entities. At the initiative of the Reserve Bank of India (RBI), the PDs were asked to put in place Value at Risk models along with the duration based measures of risk in December 2000. The regulatory response to inefficiencies in risk measurement of PDs arising out of lack of liquidity and low/no trading of several securities over a period of time was to impose a higher holding period of 30 days in VaR calculation, thereby providing a higher capital cushion as a cover for inefficient risk measurement. The overriding concern for financial stability thus contributed to higher cost of capital, with grumblings from the market.

The markets developed significantly over the years 2001-2005 with secondary market turnover showing quantum jumps. As the assets began to be churned at a faster rate, the extended time horizon came to be extensively debated during the interface between market participants and regulators. A need was thus felt to explore if a quantification of liquidity could be factored into Value at Risk models that may more efficiently measure the market risk faced by the financial firms as compared to a large time horizon. This has assumed special significance as more and more banks prepare themselves towards greater sophistication in risk measurement models in the context of the Basel II recommendations.

In this context, the paper examines the models of capturing liquidity risk in the Indian debt market. Using data on the Indian Government securities market, the paper tries to provide a Liquidity Adjusted Value at Risk (L-VaR) model that incorporates liquidity risk in Value at Risk models. The paper tests the performance of L-VaR model vis-a-vis existing VaR models. The paper is structured as follows. In Section I, the existing methodologies for incorporating liquidity risk in Value at Risk models are discussed. Section II presents a brief analysis of liquidity risk in the Indian debt market. In Section III, a Liquidity Adjusted Value at Risk Model is estimated for the Indian Government Securities market. Section IV presents the concluding observations.

The existing approaches to liquidity adjustment in Value at Risk modeling can be categorised into six broad groups.

1) Ad-hoc Approach (Lengthening Time Horizon)

The common practice of incorporating liquidity risk in VaR model is to integrate this liquidity risk by adjusting, in an ad hoc way, the time horizon according to the characteristics of liquidity of the assets considered. Indeed, if the liquidation has effectively an impact on the price, the classical VaR turns out to be insufficient because the period used for its calculation does not allow for an ‘orderly liquidation’. From then on, the lengthening of the holding period ensures an ‘orderly liquidation’. The increase of the VaR number following the extension of the holding period can therefore be directly linked to the risk of liquidity. This has been the practice in the Indian government securities market, prescribing a 30-day holding period to account for liquidity risk in contrast to the 10-day time horizon prescribed by the BIS.

2) Optimal Liquidation Approach/ Transaction Cost Approach

According to Lawrence and Robinson (1995), the best way to capture liquidity issues within the VaR would be to match the VaR time horizon with the time investor believes it could take to exit the portfolio. For example, if investors believe liquidity is a problem for the given portfolio, they could estimate the time needed to exit the positions and use this as the VaR time horizon. As this time horizon is increased (due to the illiquidity of the portfolio), the reported VaR would also increase to reflect higher risk. From an example of estimation of Value at Risk, the authors find that the largest amount of money a position could lose, with a given degree of confidence, over a one day time horizon is underestimated. Lawrence and Robinson (1995) provide a model of Value at Risk by deriving the optimal execution strategy incorporating the market risk using a mean-standard deviation approach.

Glosten and Milgrom (1985) equate the adverse selection costs to the compensation for losses to informed traders that the market maker extracts from trades with uninformed investors. This compensation directly translates into the width of the bid-ask spread. Holthausen, Leftwich and Mayers (1987 and 1990) estimate the impact of block sales of NYSE stocks on the stock prices. Their studies focus on the market impact of a large trade whose size exceeds the normal quote depth. In the same way, Bertsimas and Lo (1998) derive dynamic optimal trading strategies that minimize the expected cost of execution over an exogenous time horizon. Then, they obtain an optimal sequence of trades as a function of market conditions. Almgren and Chriss (1998) consider the problem of portfolio liquidation with the aim of minimizing a combination of volatility risk and transaction costs arising from permanent and temporary market impact. From a simple linear cost model, they build an efficient frontier in the space of time-dependant probability. They consider the trade-off of incurring a transaction cost by selling quickly vis-à-vis the exposure cost of holding on to the asset over a longer period. Their analysis leads to general insights into optimal portfolio trading, relating risk aversion to optimal trading strategy. Unlike Almgren and Chriss (1998), Hisata and Yamai (2000) turn the sales period into an endogenous variable. This model incorporates the mechanism of the market impact caused by the investor’s own dealings through adjusting Value at Risk according to the level of market liquidity and the scale of the investor’s position.

3) Liquidation Discount Approach

Within the VaR framework, Jarrow and Subramaniam (1997) provide a market impact model of liquidity. They consider a trader with an optimal liquidation problem and attempt to determine the optimal holding period by (a) estimating possible impact of trader’s own strategy on the market, (b) adding the average liquidity discount to the trader’s losses to account for the cost of not being able to sell at the mid-price, but rather settling at the bid-price, (c) also adding a correction to the lognormal VaR with the help of the mean and the standard deviation of an execution lag function. The model of Jarrow and Subramanian is intuitively appealing but difficult to implement in practice as model derivation requires additional parameters for which data are not readily available.

4) Exogenous Liquidity Approach

Bangia, Diebold, Schuermann and Stroughair (1999) provide a model of VaR adjusted for what they call exogenous liquidity defined as common to all market players and unaffected by the actions of any one participant. It encompasses such execution costs as order processing costs and adverse selection costs resulting in a given bid-ask spread faced by investors in the market. In contrast, endogenous liquidity is specific to one’s position in the market, depends on one’s actions and varies across market participants. It is mainly driven by the size of the position: the larger the size, the greater the endogenous illiquidity. The dividing line between exogenous and endogenous liquidity is the depth of the quote in the market. An investor subject to exogenous liquidity trades a quantity smaller or equal to the quote depth and does not affect the market price. He sells at the bid or buys at the ask. As he starts to trade positions larger than the quote depth, his trade price will deteriorate depending on the size of his trade. This taxonomy of liquidity, however, ignores the issue of frequency of trading which relates to the length of the time interval for which the quote depth exists. Therefore, it lacks the time dimension by assuming that the quote depth stays constant over time. Bangia et al. (op cit) argue that the deviations of this liquidation price from the mid-price are important components to model in order to capture the overall risk and derive an additive correction to a Gaussian single-asset VaR by computing the exogenous cost of liquidity.

5) Market Price Response Approach

Berkowitz (2000) highlighted that unless the potential loss arising from the liquidity risk is quantified, the models of Value at Risk would lack the power to explain the risk embedded. These costs will be more important if the market is ‘illiquid’. The first attempts to model this liquidity risk consisted in trying to associate it to various measurable quantities such as the capitalisation, the average turnover, the daily average turnover adjusted to the market capitalization, the quoted spread or even the quotation itself, the Normal Size of Block (NSB). But, because liquidity is to be considered only if it contributes to the potential loss, the ideal ‘natural’ unity of expression of this risk would be the ‘monetary’ unity of the position. The inherent concept associated to the VaR therefore seems completely adequate to take into account the liquidity risk.

6) Intraday Liquidity Risk

Le Saout (2000) distinguishes interday and intraday Value at Risk. The author proposes a new intraday measure of liquidity risk which is constructed from the return during a market event defined by a volume movement. His results indicate that we can distinguish a systemic liquidity risk, which refers to liquidity fluctuations driven by factors beyond individual investors’ control, from an endogenous liquidity risk, which refers to liquidity fluctuations driven by individual actions such as the investors’ position.

From the above models, the liquidity discount model appears to be the most comprehensive and efficient of all models. However, it remains difficult to implement due to extensive data requirements for model estimation. The transactions cost approach fails to incorporate spread risk and endogenous liquidation strategy. The exogenous spread approach fails to cover endogenous liquidity. The market response approach focuses on endogenous liquidity and neglects other dimensions of liquidity risk.

The Indian experience with Value at Risk models started in December 2000 when the Government securities market was just starting to develop and gain some depth. Since there was no mechanism as well as data to factor in liquidity risk in the Value at Risk calculations for Primary Dealers, it was decided to opt for a substantially higher holding period of 30 days.

In October 2002, the Reserve Bank of India issued a set of guidelines for banks on managing market risk that includes liquidity risk. The first step towards liquidity management included measures to put in place an effective liquidity management policy to, inter alia, spell out the funding strategies, liquidity planning under alternative scenarios and prudential limits. Banks can make use of key ratios such as Loans to Total Assets, Loans to Core Deposits, and Borrowed Funds to Total Assets to assess their liquidity position. The RBI has prescribed a format in this regard under the ALM system, which needs to be adopted for measuring cash flow mismatches at different time bonds. The cash flows should be placed in different time buckets based on projected behavior of assets, liabilities and off-balance sheet items. All banks are required to produce a contingency funding plan approved by their Asset Liability Committees (ALCO). The plan is to be submitted annually as a part of the liquidity and capital plan that would be reviewed quarterly. ALCO will have the authority to implement the contingency funding plan. It can also amend

the plan with the approval of the Risk Management Committee, wherever it feels necessary, to meet the changing conditions.

The Indian debt market underwent a complete transformation during 1997-2005. The secondary market yields, which were kept artificially low in an administered interest rate regime till the early 1990s, began to be market determined. With the introduction of Primary Dealers in 1996, the improvements in settlement systems and the introduction of Liquidity Adjustment Facility ( LAF) by the Reserve Bank in June 2000 and the institution of the central bank repo corridor, the market saw tremendous expansion over 1997-2004. The outright transactions have increased almost ten fold over past seven years. The growth of repo market was also phenomenal - it grew faster than the outright market and as a result the share of outright transactions in total transactions in secondary market fell from 82 per cent in March 1997 to 44 per cent in March 2005 (Table 1).

Within this growing depth of the market, lay, however, liquidity holes. Only a few securities were traded in the market on a regular basis. This illiquidity has been of serious concern to banks and other financial market participants, as there is no established mechanism to price the cost of illiquidity. The liquidity of a bond is typically measured through (a) number of trades, (b) trade volume, (c) turnover ratio of a bond (trade volume as a ratio of outstanding amount) and (d) the bid–ask spread.

(Rupees crore)

In the Indian context, our study compares two government dated securities prefixed by coupon and suffixed by year of maturity. The first one, 8.07%GS 2017 was the most traded in 2003-04 accounting for 5.28 per cent of the secondary market outright turnover. The other security is 9.39% GS 2011, which was moderately traded accounting for 1.57 per cent of total turnover in 2003-04, but for which indicative bid-ask spread are available at a fairly representative frequency (Table 2).

The spread behaviour of the securities is presented in Tables 3 and 4 on a monthly frequency for the financial year 2003-2004 (April-March). Data on the number of executed trades, average trade size, average monthly price and yield and turnover are also presented.

The relative spread seems to be negatively correlated to turnover. An increase in the volume of trade results in a lowering of the bid-ask spread. An increase in trade size produces a positive impact on spread, indicating the existence of an endogenous liquidity cost of thin markets. The usual inverse relation between yield and price gets reflected in the correlation matrices presented in Tables 5 and 6.

The end-March 2004 Value at Risk and Liquidity adjusted Value at Risk is presented for both securities. Market risk calculations for the Indian debt market were done by taking into account both the market and liquidity components to total market risk. Of principal interest here is the marginal impact of the liquidity component, as shown in Table 7. The standard parametric VaR model is estimated as normally distributed with 99 per cent tail probability. The estimated volatility is the conditional volatility estimated with the help of GARCH (1,1) model.

For the highly liquid security, the market risk for a 1-day VaR was 0.779 per cent, while the Liquidity adjusted VaR (L-VaR) was 0.828 per cent. For the 9.39 GS 2011, which had a lower turnover, the market risk based on 1-day VaR was 0.541 per cent while the L-VaR was 0.641 per cent. Thus the liquidity risk component for 8.07%

GS 2017 was 5.92 per cent of total adjusted Value at Risk (L-VaR) while for 9.39% GS 2011, the liquidity risk component turned out to be much higher at 15.6 per cent. This indicates that the liquidity risk in the Indian debt market differs significantly between a highly traded instrument and a less traded Government security. The method of using bid-ask spread data for deriving the liquidity component thus gives some understanding of latent liquidity risks in the Indian debt market.

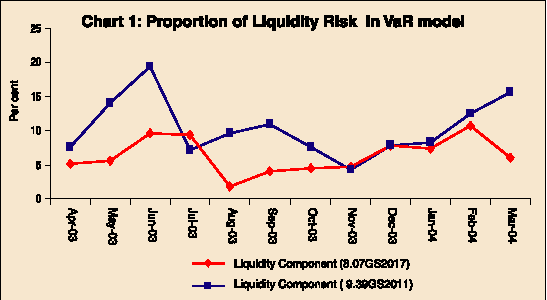
We also compare month end estimates of Value at Risk with and without the liquidity component (Chart 1). The Chart plots the proportion of liquidity risk in Value at Risk calculation and shows the month end component of liquidity risk as a proportion of the L-VaR figures arrived at after adjusting for liquidity. The empirical exercise demonstrates that the liquidity risk component can be as high as 20 per cent of the Value at Risk measure estimated by traders to judge the risk in their portfolio. It is also observed that the liquidity risk in the moderately traded security was higher than the security with the highest turnover. It, therefore, seems quite likely that liquidity risk may be still higher for many lowly traded securities in the Indian debt market.

Liquidity risk is an aspect of market risk that has been largely neglected by standard value at risk models. This negligence is partly due to the fact that no single measure can effectively capture the various aspects of liquidity in financial markets. In this paper, we apply the Liquidity Adjusted Value at Risk model provided by Bangia, Diebold, Schuermann and Stroughair (1999) to the Indian debt market.

While the overall market liquidity is being monitored and fine tuned by the Reserve Bank of India through its Liquidity Adjustment Facility (LAF) and Open Market Operations(OMO), pockets of illiquidity continue to exist in the market. Large exposures in illiquid assets can be potentially harmful as they cannot be offloaded at market related rates. In this paper, a measure of Liquidity Adjusted Value at Risk based on the bid-ask spread is presented for the Indian debt market and the liquidity risk is found to be an important component of the aggregate risks absorbed by the financial institutions.

The liquidity risk is characterised through an adjustment based on the average weighted price spread of Government securities. Given the data limitations in the Indian debt market, this paper can be treated as a starting point in integrating liquidity risk in a VaR framework. As the market develops and trades become more frequent, the model can be improved upon by trying to quantify simultaneously the exogenous liquidity risk and the endogenous liquidity risk.

Almgren, R. and N. Chriss (1999), ‘Optimal Execution of Portfolio Transactions’, Working Paper, The University of Chicago, Department of Mathematics, April.

Bangia, A., Diebold, F., Schuermann, T. & Stroughair, J. (1999), ‘Modeling Liquidity Risk with Implications for Traditional Market Risk Measurement and Management’, Working Paper, The Wharton School-University Pennsylvania .

Berkowitz, J. (2000), ‘Incorporating Liquidity Risk into VaR Models’, Working Paper, Graduate School of Management, University of California, Irvine, September.

Bertsimas, D. and Lo, A. W. (1998), Optimal Control of Execution Costs,

Journal of Financial Markets, 1-50.

Black, F. (1971), ‘Towards a Fully Automated Exchange : Part 1’, Financial Analyst Journal, 27, 29–34.

Dowd, K.(1998), Beyond Value at Risk : The New Science of Risk Management, ed. John Wiley & Son.

Glosten, L. and Y.P. Milgrom, (1985), "Bid, Ask and Transaction Prices in a Specialist Market with Heterogeneously Informed Traders", Journal of Financial Economics, No.14, March (71-100).

Hisata, Y. and Y. Yamai, (2000), ‘Research Toward the Practical Application of Liquidity Risk Evaluation Methods’, Discussion Paper, Institute for Monetary and Economic Studies, Bank of Japan.

Holthausen, R.W., Leftwich, R.W. and Mayers, D. (1987), "The Effect of Large Block Transactions on Security Prices: A Cross Sectional Analysis,"

Journal of Financial Economics, 19, 2, 237-267.

Jarrow, R. and Subramaniam, A. (1997), ‘Mopping up Liquidity’, Risk 10(12), December 1997, 170-173.

Lawrence, C. and G. Robinson (1995), "Value at Risk: Addressing Liquidity and Volatility Issues, Capital Market Strategies, 9, November, pp. 24-28.

Le Saout, E. (2000), Beyond the Liquidity : From Microstructure to Liquidity Risk Management, Ph. D thesis,University of Rennes 1, November.

Reserve Bank Of India (2004), Handbook of Statistics of the Indian Economy, Mumbai, India.

Reserve Bank of India, Annual Report, Various Years.