Jibin Jose, Himani Shekhar, Sujata Kundu,
Vimal Kishore and Binod B. Bhoi^*

Received on: June 11, 2021
Accepted on: September 23, 2021

This study develops a suite of inflation forecasting models for India and examines their forecasting performance over one-quarter ahead and four-quarters ahead horizons. Besides testing the suitability of a Phillips curve relationship in India for forecasting Consumer Price Index (CPI) inflation, it also uses relevant autoregressive integrated moving average (ARIMA) and structural vector autoregression (SVAR) models. Out of sample forecasts suggest that seasonal ARIMA (SARIMA) models outperform others for one-quarter ahead forecasts, whereas variants of Phillips curve work better for four-quarters ahead forecasts in the case of inflation excluding food and fuel. To account for significant variations in inflation characteristics across CPI components, disaggregated level (food, fuel and excluding food and fuel inflation) forecasts are also generated and then combined to compare with aggregate level forecasts. The results show that disaggregated inflation forecasts based on univariate models generally underperform in comparison to aggregate level forecasts. Disaggregated level forecasts that incorporate Phillips curve dynamics, however, perform better vis-à-vis direct forecasts over a longer forecast horizon, validating the utility of disaggregated level analysis of inflation in India. While SVAR models do not score well on forecasting performance, they provide useful insights for evaluating the impact of different shocks on inflation.

JEL Classification: E31, E37, E52, E58

Keywords: Inflation forecasting, ARIMA model, Phillips curve, SVAR model, disaggregated forecast, inflation targeting

Introduction

Modelling the dynamics of inflation unerringly for generating reliable inflation forecasts has all along been a daunting challenge for researchers. Given the significant transmission lags in monetary policy, central banks often need to undertake forward-looking policy decisions based on their assessment of the outlook for key macroeconomic variables in order to be able to achieve their policy objectives. Therefore, more accurate, reliable and unbiased the forecasts are, better could be the policy outcomes. Under an inflation targeting monetary policy framework, where inflation forecast acts as the intermediate target, generating reliable inflation forecast assumes even greater importance as systematic forecast errors can hinder the optimal conduct of monetary policy and thereby undermine policy credibility. Accurate inflation forecast is of importance even for economic agents in forming their inflation expectations while negotiating wage-price contracts and also for understanding how policy makers might react in future in their endeavour to achieve the objective of price stability. Achieving and maintaining inflation target on a sustained basis, thus, depends crucially on the accuracy of inflation forecasts.

Given the importance of inflation forecasting for the conduct of monetary policy, central banks use an array of models – time series models such as univariate (ARIMA-based) and multivariate (unconstrained and structural vector autoregressions) models and macro-economic models incorporating measures of economic slack and inflation expectations (especially variants of Phillips curve models) for forecasting and policy analysis purposes. Often a simple random walk model or its variants are found to outperform complex structural econometric models in forecasting (Atkeson and Ohanian, 2001; Garnier, Mertens, and Nelson, 2015). However, some of the cross-country studies, both for advanced and emerging market economies (EMEs), have found variants of vector autoregression (VAR) models also performing relatively well (Banbura, 2010; Duncan and Martínez-García, 2015; Mandalinci, 2017; Duncan and Martínez-García, 2019; Iyer and Sen Gupta, 2019). Furthermore, in the case of advanced economies, studies have shown that models based on Phillips curve are more successful in modelling and forecasting inflation (Coibion and Gorodnichenko 2015; Kabukçuoğlu and Martínez-García, 2018), notwithstanding the overwhelming proliferation of research in the last decade or so arguing that the “Phillips Curve is dead” (Blanchard et al., 2015; Blinder, 2018). Ultimately, inflation forecasting is a country- and time-specific issue, and no single model is sufficient. Moreover, models used for forecasting must be regularly updated to take into account dynamic changes in the inflation process and also new sources of data as and when they become available.

India formally adopted a flexible inflation targeting (FIT) framework in June 2016, following which there has been a shift in the inflation metric from the Wholesale Price Index (WPI) to the Consumer Price Index (CPI). CPI-Combined (CPI-C) inflation is the nominal anchor under this framework, and the Reserve Bank of India (RBI) is mandated with the objective of achieving a 4 per cent inflation target over the medium term¹ with the upper tolerance limit of 6 per cent and the lower tolerance limit of 2 per cent. It has been argued that an established FIT framework with a credible long-run inflation target would serve as an anchor to expectations, and therefore, would provide an effective strategy for dealing with the second-round effects of supply shocks in the Indian scenario (Benes, et al., 2016). As per the mandate of the amended RBI Act, 2016 to publish a half-yearly Monetary Policy Report (MPR) including inflation forecast for 6-18 months, RBI developed a macroeconomic model – Quarterly Projection Model (QPM) – for generating medium term projections and policy analysis (RBI, 2021).² In the short-term, nowcasting using high frequency data and forward-looking surveys, and forecasts up to three-quarters following a bottom-up approach employing alternate models are used. In this endeavour to generate accurate and reliable forecasts, there has been a growing interest in exploring different aspects of inflation forecasting in the Indian context in recent times (Dholakia and Kandiyala, 2018; Pratap and Sengupta, 2019; John, Singh and Kapur, 2020). Moreover, as observed by many practitioners, inflation forecasting has become an increasingly challenging task and the performance of models varies depending upon several factors (Stock and Watson, 2008; Stock and Watson, 2010; Pratap and Sengupta, 2019; John, et al., 2020). Therefore, continous evaluation of forecast performance across models and over time is necessary.

This paper intends to contribute to this strand of literature by developing a suite of inflation models and examining the appropriateness of alternative models based on their forecasting performance over one-quarter ahead and four-quarters ahead horizons using CPI-C inflation data. The time period covered for empirical analysis in this paper begins from 1996-97:Q1 (mainly due to the availability of quarterly GDP data since then) and ends in 2019-20:Q4 (recognising issues in data reporting during Q1:2020-21 following the COVID-19 induced lockdown). Models are estimated for the period 1996-97:Q1 to 2017-18:Q3 and out of sample forecasts are generated for the period 2017-18:Q4 to 2019-20:Q4, which not only allows forecast evaluation over a reasonable period of time but also helps in selecting the appropriate forecasting model at different time horizons. We employ three approaches – univariate models, structural VAR models and Phillips curve (PC) based models – and extend the analysis to three major sub-components of inflation, viz., food, fuel and excluding food and fuel (i.e., ‘core inflation’ henceforth). The major motivation for such an approach is rooted in the specific structural characteristics of the Indian economy – large share of food in the CPI along with higher food price volatility as well as high sensitivity of core inflation to international crude oil prices. In the face of large relative price movements and idiosyncratic price shocks, aggregate measures of inflation could mask the underlying inflation dynamics. Under such circumstances, a model based on aggregate inflation may run into the risk of producing bias in inflation projections. While the international evidence in this regard is mixed (Hendry and Hubrich, 2006; Huwiler and Kaufmann, 2013), recent findings for India suggest that directly forecasting the aggregate measure is better in case of univariate models (Pratap and Sengupta, 2019). In this endeavour, this paper attempts to model and forecast not only headline inflation (direct approach) but also disaggregated level inflation by factoring in macroeconomic and sector-specific determinants (indirect approach). Furthermore, a comparison is made between models regarding the performance of forecasts generated from direct versus indirect methods over one-quarter ahead and four-quarters ahead horizons for choosing the best performing model. Identifying models that perform better in forecasting inflation at different horizons also requires to develop an array of models.

The analysis undertaken in this paper is significant on the following counts: first, our findings corroborate the existence of the PC relationship in the Indian context. Second, it finds that while univariate models perform better in forecasting one-quarter ahead inflation, the PC-based models tend to outperform the former for four-quarters ahead forecast horizon in the case of core inflation. Further, our analysis suggests that the performance of forecasts generated from direct versus indirect approaches depends on the underlying model and the forecast horizon – disaggregated level forecasts incorporating Phillips curve dynamics are generally better compared to aggregate level inflation forecasts. The rest of the paper is organised as follows: Section II provides a descriptive analysis of inflation in India; Section III discusses the extant literature; Section IV lays out the empirical strategy and estimation; Section V presents the forecast evaluation; and Section VI concludes the paper.

Section II
Inflation in India – Some Observations

India’s inflation developments during the past two decades (1996-97:Q1 to 2019-20:Q4) reveal significant variations in both the level and volatility of inflation at the aggregate and disaggregated level (Table 1).³ Headline inflation⁴ ranged between a high of 17.9 per cent in 1998:Q4 and a low of 0.5 per cent in 1999:Q4. Further, measures of skewness and kurtosis together imply that although the headline inflation distribution showed a positive skew during this period suggesting that most inflation outcomes generally remained below the mean, there were also phases when inflation deviated significantly from its mean. A disaggregated picture of CPI inflation – food, fuel and core – provides further insights into the overall inflation dynamics. Notwithstanding similar mean inflation, the food group (with its weight of 45.9 per cent in the CPI-C⁵) is much more volatile than core inflation⁶ (weight of 47.3 per cent), which in turn, imparts significant volatility to headline inflation. On the other hand, the fuel group, though has a lower weight (6.8 per cent), recorded the highest average inflation and volatility over the sample period.

The period since the mid-1990s also witnessed two major shifts in the monetary policy regime: multiple indicators approach (during 1998-99 to 2013-14) and flexible inflation targeting (FIT) preceded by a transitional glide path from 2014-15⁷. The behaviour of inflation has been distinct during the two regimes – inflation was much more volatile during the multiple indicators regime as compared to the FIT regime, despite the latter period experiencing many structural shocks such as demonetisation and the introduction of goods and services tax (GST) (Chart 1a). The disinflation ahead of FIT was broad-based, driven by easing in domestic food inflation on the back of record food grains and horticulture production as well as sharp reduction in international crude oil prices, even as their benefits were not fully passed on to domestic petroleum product prices. Building on this disinflation, credibility gains accruing to monetary policy on account of its focus on an inflation target together with a stable exchange rate resulted in a relatively low and steady inflation outcome during the FIT period (RBI, 2021).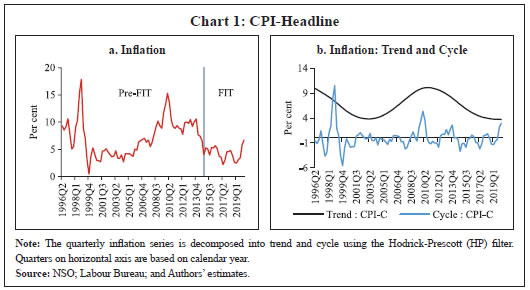

Measured (actual) inflation, however, does not fully reflect the underlying changes in the inflation process; i.e., whether the observed changes in inflation are driven by the long-term ‘trend’ component or short-term ‘cyclical’ fluctuations, which is crucial for understanding future inflation as well as the conduct of monetary policy. Trend inflation is viewed as the level to which actual inflation outcomes are expected to converge after short-run fluctuations die out (Behera and Patra, 2020), whereas the short-run fluctuations emanate from a variety of sources/price shocks mainly on the supply side. The literature suggests that under univariate framework, the overall dynamics of inflation are largely dominated by the trend component (Stock and Watson, 2007). The precise measurement of trend inflation, however, is an empirical issue (refer to Behera and Patra, op cit. for an exposition). A simple decomposition of headline inflation using the Hodrick-Prescott (HP) filter reveals that the sharp fall in trend inflation has been the driver of the general easing of headline inflation during the FIT period⁸. However, it can be observed that the HP trend is time-varying, while short-term fluctuations follow a stationary process (Chart 1b). In addition, short-run and long-run components of inflation are crucial in estimating inflation persistence, which has significant implications for the design of monetary policy (Ascari and Sbordone, 2014).

Aggregate level analysis, however, may not fully reflect the observed changes in the volatility and persistence of the sectoral or idiosyncratic (such as food and fuel) price shocks, which are often used for calibrating model-based forecasts for policy purposes. In view of this, an analysis of the trends and cyclical components of the major groups of CPI may be necessary. It can be observed that the trend components of CPI major groups which were widely varying prior to FIT regime have become more aligned since the transition to FIT, suggesting anchoring of inflation expectations (Chart 2a). In contrast, cyclical components of inflation, which are stationary in nature, implying they even out over time, continue to exhibit significant fluctuations, albeit with some moderation in amplitudes, thus imparting volatility to actual inflation (Chart 2b). The determinants of sectoral price dynamics, therefore, should be taken into account in inflation modelling and forecasting exercises.

The need for examining sectoral price dynamics may also be necessary from the perspective of understanding the sources of fluctuations in measured headline inflation, i.e., the drivers of inflation given the relative importance of food and non-food items (as represented by their weights in CPI) in the household consumption basket as well as the relative price movements over time. This is because headline inflation is derived from CPI-C, which in turn, is compiled following a bottom-up approach.⁹ From the monetary policy perspective, if relative price movements are large, persistent and not offsetting, they impinge on monetary policy setting as they can have a lasting influence on inflation expectations through second-round effects (RBI, 2021).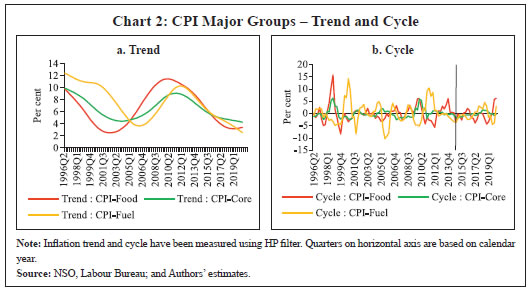

It can be observed that the food group has contributed significantly to headline inflation all through the years (Chart 3a). This is not surprising given the higher weight of food in the CPI (45.9 per cent) and frequent supply side shocks that affect food production leading to higher volatility in food prices. Food price inflation in India has also been observed to be persistent, for instance during the five-year period post-global financial crisis (GFC), reflecting a combination of supply and demand factors (Mohanty, 2014). On the other hand, the contribution of core component to CPI appears to be largely steady throughout. Moreover, relative food prices (the ratio of food to non-food price indices) trended up during 2005-2016, before showing some moderation during the FIT period reflecting record food production and improved supply management by the government (Chart 3b). Fuel (including petrol and diesel) prices, on the other hand, exhibits significant co-movement with international crude oil prices due to India’s large dependence on crude imports. Thus, given that both food and fuel prices in India are characterised by distinct inflation process (prone to supply shocks with risks of generating second round effects), aggregate level analysis may need to be strengthened with the modelling of disaggregated level inflation for generating reliable inflation forecasts for policy purposes, which is the focus of this paper.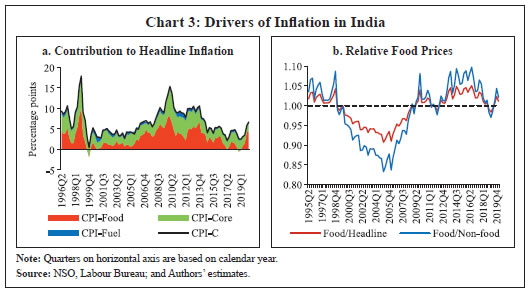

Section III
Review of Literature

III.1: Time Series Models

Univariate Models

Many time series processes can be expressed as a parsimonious autoregressive integrated moving average (ARIMA) model after appropriate data transformation and differencing. ARIMA models employ a combination of autoregressive (past values of itself) and moving average (lagged values of a ‘white noise’ error term) models. Given the simplicity and the requirement of just one data series, ARIMA based forecasting has become one of the most common forecasting approaches. Further, by giving more weight to near-term outcomes, ARIMA models are able to beat more complicated structural models in terms of short-term forecast performance (Litterman, 1986; Stockton and Glassman, 1987; Meyler, et al. 1998). Also, unlike economic models that are restrictive in their theoretical formulations, which can inflict improper restrictions and specifications on the structural variables, ARIMA models have no such restrictions imparting the necessary flexibility to capture the dynamic properties and, thus, possess significant advantages in short-run forecasting (Saz, 2011). These models are also flexible to include deterministic effects (interventions), outliers, trading day and festival effects (Gómez and Maravall, 1998). ARIMA models can also handle seasonality in time series data and hence, forecasters give similar importance to the simplest univariate forecasting methods as econometric models.

However, these models have certain drawbacks as they do not ingrain any underlying theoretical or structural relationships. ARIMA models are primarily ‘backward-looking’ which means that they are poor at predicting turning points, unless the turning point represents a return to a long-run equilibrium (Meyler, et al. 1998). Furthermore, ARIMA models are considered to be too simplistic, subjective, agnostic and atheoretic in nature (Saz, 2011). To overcome these limitations of univariate forecasting, time series models are often extended to include other variables in the form of single equation models with exogenous explanatory variables or a structural or non-structural system of equations.

Multivariate Models

Within multivariate models, a notable approach is to model multiple time series predictor variables simultaneously along with inflation using high-dimensional VARs (Stock and Watson, 2008; Bańbura, et al. 2010; Canova, 2011). One of the principal uses of a VAR model is to generate forecasts. These models involve constructing subsidiary models for the predictor variables, or alternatively, modelling inflation and the predictors jointly and iterating the joint model forward while imposing certain parameter restrictions which could involve complex macroeconomic structure and linkages. The merit of these models over univariate approaches is that of using additional information available from other related time series as well as theory-based structural relationships among them to obtain better forecasts. Out-of-sample forecasts are obtained via forward iteration which in practice is done by a “rolling one-period-ahead” forecast where the estimated VAR coefficients are updated each period in order to account for the latest data release of the variables.

III.2: Macro-economic Models

Another important modelling framework within the class of economic models is the Phillips curve¹⁰. The study of the nature of the PC trade-off has non-trivial implications for the conduct of monetary policy and business cycle fluctuations, and is routinely undertaken with the objective of modelling and forecasting inflation. The literature on PC has undergone significant changes overtime, with the New Keynesian Phillips Curve (NKPC) and its appealing theoretical microfoundations gaining popularity and becoming a standard feature of many analyses (Nason and Smith, 2008; Dees et al., 2009). The PC-based models happen to be the most widely used for inflation forecasting after the univariate approaches.

III.3: The Indian Scenario

Several studies have used the univariate approach to forecast inflation in the case of India. Some of the studies have used ARIMA models as benchmark to evaluate forecasting performance of their economic models (John, et al. 2020), while others, like Pratap and Sengupta (2019) have evaluated a set of models using CPI data for forecasting performance and concluded that the best forecasting performance is achieved by the SARIMA model of the form (3,1,1) (2,1,1). On the other hand, Srivastava (2016) uses ARIMA based approaches and compares direct and indirect forecasts of food inflation with the conclusion that a disaggregated approach performs better in the case of food inflation.

A few papers in the Indian context have used VARs not only to estimate or determine inflation but also to study the factors that influence inflation expectations. An analysis of core inflation in a structural VAR (SVAR) framework with a vertical long-run supply curve as the identifying condition points towards the role of both demand and supply side shocks in inflation dynamics (Goyal and Pujari, 2005). The results using quarterly data from 1996-97:Q1 to 2013-14:Q3 identify crude oil price, output gap, fiscal policy and monetary policy as the determinants of inflation in India along with pointing out significant changes in India’s inflation dynamics after the global financial crisis (Mohanty and John, 2015). Further, a 7-variable SVAR framework finds evidence of inflation expectations anchoring with the Reserve Bank communications as well as headline inflation affecting inflation expectations in the short-run and core inflation dominating in the long-run (Goyal and Parab, 2019).

Empirical explorations on PC in the Indian context in the last two decades have been mainly influenced by two strands of the literature: (i) The first one is an augmented PC put forth by Gordon (1998), generally referred to as the triangle model of inflation, in reference to the three basic determinants of inflation in the model – inertia, demand, and supply side factors; (ii) The second one is a modified version of the purely forward-looking NKPC (Gali and Gertler, 1999; Gali, Gertler, and Lopez-Salido, 2005). Such an ad-hoc modification was necessitated because of the lack of empirical support for the purely forward-looking NKPC as lagged inflation remained an important determinant of inflation dynamics. Consequently, a hybrid PC was born – with both forward and backward-looking components in the data generating process. While a majority of the empirical work using Indian data has been centred around these two approaches, one cannot fail to observe that there is considerable heterogeneity in the specifics of each of the studies, leading to a range of point estimates of the slope of the PC. This heterogeneity primarily arises due to the following factors: assumptions on the data generating process (inclusion/exclusion of the forward-looking component); the choice and structure of the economic activity variable [Index of Industrial Production (IIP) versus GDP]; the time period; and the specific econometric methodology used. However, despite these apparent differences, there is a general consensus on the existence of a PC relationship in the Indian scenario.

Several papers have estimated the backward-looking PC similar to Gordon (1998). Using this approach on annual data from 1970-71 to 2000-01, Kapur and Patra (2000) estimate the sacrifice ratio – output forgone to achieve lower inflation – and find that lagged inflation and the demand variable, proxied by the output gap, are significant in determining inflation. Some studies using the backward-looking version of PC on annual data during 1994-2005 (Srinivasan, Mahambare and Ramachandran, 2006) and hybrid version of PC on annual data from 1996-2007 (Mishra and Mishra, 2012) find no evidence for the PC relationship, while some others find evidence for the same for the sub-sample of 2004-2009 (and not for the period 1997-2003) (Singh, Kanakaraj and Sridevi, 2011) and statistically on the borderline during the period 1996-2005 (Dua and Gaur, 2009). However, once this period of study is extended even slightly or a longer horizon is considered, the relationship comes back alive as can be found in Paul (2009), Mazumder (2011), and Patra and Kapur (2012).

Similarly, Patra and Ray (2010) explore the dynamics of inflation expectations and find output gap to be one of the determinants along with lagged inflation, food and fuel price changes and real interest rate. Revisiting the PC relationship under the triangle model, Kapur (2013) concludes that the demand variable is significant even when supply shocks are not incorporated, and that rainfall shortage and minimum support price (MSP) affect inflation. Further, PC based forecasts outperform random walk model forecasts. Patra, Khundrakpam and George (2014) estimate a hybrid augmented PC and find the coefficient of output gap to be positive and significant as well as a rise in the contribution of expectations to inflation persistence, measured by the coefficient of one-period lead inflation, in the post-crisis period. Ball, Chari, and Mishra (2016) employ a backward-looking PC and explain inflation rate as a function of slow-moving average of past inflation and the deviation of output from its trend.

A notable observation is that in most of the empirical work mentioned so far, inflation was represented by the WPI as the formulation of monetary policy was anchored on movements in WPI inflation¹¹. In contrast, a number of recent papers (such as Chinoy, et al. 2016; Behera, et al. 2017; Pattanaik, et al. 2019; Sharma and Padhi, 2020; Patra, et al. 2021) have estimated similar models using the CPI based inflation in view of the switch from WPI to CPI as the inflation metric under the FIT framework in India since 2016. While Chinoy, et al. (2016) and Pattanaik, et al. (2019) explore inflation dynamics in a standard time series framework with the latter focusing exclusively on inflation expectations, Behera, et al. (2017) estimate the PC using state-level data; Sharma and Padhi (2020) propose an alternative indicator of economic slack that captures demand conditions efficiently to forecast core inflation; Patra, et al. (2021) explicitly address the time-varying and convexity properties of PC – all these papers corroborate the existing evidence on PC relationship in India. A survey on the range of point estimates of the slope coefficients and methodologies used in the literature suggests that all the studies have remained close to Gordon (1998) and Gali and Gertler (1999) in terms of the econometric methodology employed – choosing either ordinary least squares (OLS) or Instrumental Variables-Generalised Method of Moments (IV-GMM) techniques (Table 2).

Section IV
Empirical Strategy and Estimation

IV.1 Univariate Models

An AR (p) process may be represented as a combination of its past values and a “white noise” error term:

where ε_t is a white noise process with zero mean and variance σ², B is the backshift operator and φ(B) is polynomial of degree p representing the AR terms. It models a time series as a function of its past values. Partial autocorrelation function (PACF) plots are used to take a view about the order of polynomial p.

Similarly, an MA (q) process may be represented as a weighted average of a “white noise” series:

where, ε_t is a white noise process with zero mean and variance σ², B is the backshift operator and θ(B) is polynomial of degree q representing the MA terms. Autocorrelation function (ACF) plots are used to take a view about the order of polynomial q.

When a time series is related to its past values as well as past residuals, a mixed ARMA model can satisfactorily describe it. In general, fewer parameters are required to be estimated in this case compared to a pure AR or pure MA model. An ARMA (p, q) can be represented as:

A parsimonious ARMA (p, q) model may perform well in forecasting if inflation is stationary (Ang et al., 2007). In case of non-stationary series (as is the case with CPI data in India, Appendix Table A1b), an extended form of ARMA models, i.e., ARIMA, where differencing is done to make the data stationary, may describe the time series adequately. ARIMA combines autoregressive and moving average models and can be represented as:

where, ε_t is a white noise process with zero mean and variance σ², B is the backshift operator, φ(B) and θ(B) are polynomials of degree p and q representing AR and MA terms, respectively, and d represents the order of integration that make the data stationary (Pankratz, 1983; Meyler, Kenny and Quinn, 1998). The ARIMA model expects the input time series to be non-seasonal or seasonally adjusted. Many time-series data, on the other hand, show seasonal fluctuations which may be used to supplement any forecasting information contained therein. The characterisation of seasonal series occurs by a strong serial correlation at the seasonal lags (of four and eight) in the case of CPI-headline and CPI-food in India (Appendix Table A2). Therefore, in this study we have attempted both ARIMA and Seasonal ARIMA (SARIMA) models to forecast inflation. SARIMA is a generalised form of ARIMA that supports the seasonal component in time series (Box and Jenkins, 1976). Researchers suggest that it may be irrational to assume the seasonal component to repeat itself in the same way cycle after cycle in practice (Özmen and Şanli, 2017). SARIMA models allow for irregularity in the seasonal pattern from one cycle to the next (Brockwell and Davis, 1991). While the process of seasonal adjustment may often be regarded as an integral part of modelling framework, there is always some loss of information from seasonal adjustment even when the seasonal adjustment process is properly conducted (IMF, 2017). Furthermore, de-seasonalising the data may remove certain peaks and troughs that may contain useful insights and may also come in conflict with economic theory (Depalo, 2009). SARIMA models thus assume significance in the forecasting literature.

A SARIMA model is generally represented as SARIMA (p, d, q) (P, D, Q), with p standing for the non-seasonal autoregressive order, d standing for the non-seasonal integration order and q for the non-seasonal moving average order. In the seasonal part, P stands for the seasonal autoregressive order, D stands for the seasonal integration order, Q stands for the seasonal moving average order and m for the period or length of the season (in the monthly case 12, in the quarterly case 4). It can be expressed as follows: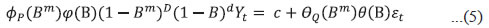

where, Φ_P(B^m) and θ_Q (B^m) are polynomials of orders P and Q, respectively.

There are two approaches to identify ARIMA models – the Box-Jenkins methodology and the penalty function statistics such as the Akaike Information Criterion (AIC), Schwarz Criterion (SC) and Hannan Quinn Criterion (HQC). The Box-Jenkins methodology infers the correct form of ARMA model from the sample autocorrelogram, partial autocorrelogram and inverse autocorrelogram plots. However, these plots are often difficult to interpret in the case of higher order mixed ARMA models. Additionally, presence of seasonality (Gómez and Maravall, 1998) and random noise in time series (Meyler, et al. 1998; Saz, 2011) further complicates Box-Jenkins model identification. Therefore, penalty function statistics, which is computationally simpler and objective, is often preferred for identifying ARIMA models.

Accordingly, in this paper, our model identification is based on the AIC penalty function criteria (Brockwell and Davis, 1991; Burnham and Anderson, 2004). We estimate ARIMA using the maximum likelihood-based techniques on the log transformed CPI data for the sample period 1996-97:Q1 to 2017-18:Q3¹² and then forecast one-period ahead and four-periods ahead inflation¹³. We also estimate SARIMA models for the same period as an alternative to the ARIMA model to check for any improvement in the forecasting performance in view of the observed seasonality in food prices in India.

The identified model satisfies the standard diagnostic checks such as autocorrelation and heteroscedasticity on residuals (Appendix Table A3). The models chosen for the headline and three major groups of CPI based on AIC are presented in Table 3.

IV.2 Structural Vector Auto Regression (SVAR) Models

In order to introduce structural characteristics into the time series, a four variable SVAR model is estimated on quarterly data from 1996-97:Q1 to 2017-18:Q3, which apart from CPI-C/CPI-Core includes nominal exchange rate (INR-USD), real output or gross domestic product (GDP) and weighted average call money rate (WACR)¹⁶. Price of the Indian basket crude oil and absolute rainfall deviation from long period average (LPA) are incorporated as the two exogenous variables in the model given their significance in influencing India’s inflation dynamics (Chand 2010; Sonna et al. 2014; Mohanty and John 2015; Anand et al. 2016).¹⁷ All the variables, except WACR and rainfall deviation, are de-seasonalised using Census X-13ARIMA, converted to their natural logarithms, and used in their first-differenced forms [i.e., quarter-on-quarter change (q-o-q)] in the model as they are non-stationary. Stationary property of the variables is tested by employing the augmented Dickey-Fuller test of unit roots (Appendix Table A1b).¹⁸

The choice of the variables and the structural identification restrictions that the model assumes for the purpose of estimation closely resemble that in the available literature (Christiano, Eichenbaum and Evans, 1999; Kim and Roubini, 2000; Uhlig, 2005; Mohanty and John, 2015). The model adopts the following ordering of the variables {INR – USD_t, GDP_t, CPI_t, WACR_t} in their first-differenced form (barring interest rate) and uses the recursive identification method for the identifying restrictions in line with Eichenbaum and Evans (1995), and Christiano, et al. (1999).¹⁹ INR-USD exchange rate is considered to be the most pre-determined variable in the model and a shock to exchange rate impacts all the variables contemporaneously. It is assumed that the real GDP in the economy responds to exchange rate variations and crude oil price movements. Domestic price is assumed to be sensitive to exchange rate variations and changes in real GDP. The monetary policy represented by WACR responds contemporaneously to all the variables. In this type of models, it is generally assumed that the central bank of the economy looks at the current prices and output, among other indicators, when setting the monetary policy instrument at time t. The recursiveness assumption implies that exchange rate, output and prices respond only with a lag to a monetary policy shock. While such an assumption has attracted a lot of attention and debate in the literature, abandoning the assumption may also lead to a substantial cost, in the sense that the identifition of a broader set of economic relations becomes complicated (Christiano, et al. 1999).

Accordingly, let Y_t denote a k X 1 vector of {INR – USD_t, GDP_t, CPI_t, WACR_t} at time t. Considering the structural identifying restrictions stated above, the model in a VAR framework can be written as: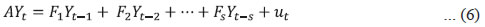

where, u_t is a k X 1 vector of structural shocks following N = (0,Σ); Σ = diag (σ_j); Fi is a (k X k) matrix of parameters for 1, 2 ,...,s; while matrix A is the contemperaneous matrix (F_o)

For identifying the above model, k(k + 1)/2 restrictions are required to be imposed on A matrix, of which k restrictions could be satisfied by normalising the diagonal elements of A to unity. In our model k = 4. Therefore, we need to impose 6 additional restrictions on the contemporaneous correlations for identification of the four structural shocks (exchange rate shock, output shock, price shock and monetary policy shock). This is done by specifying A as a lower triangular matrix.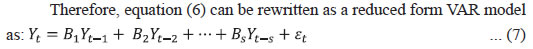

where, B_i = A^-1 F_i and ε_t follows N = (0,I).

This model is estimated on two measures of inflation: Model 1 with CPI-C as the headline inflation measure and Model 2 with CPI excluding food and fuel as the measure of core inflation. The lag lengths for the models are chosen based on the AIC and SC criteria. The models satisfy the stability test (roots of characteristic polynomial were inside the unit circle) as well as the residual autocorrelation test (Appendix Tables A4.1 and A4.2).

The structural impulse response functions (IRFs) of inflation with respect to the exchange rate shock, output shock and policy rate shock broadly meet our expectations (Chart 4). On transformation [of standard error (SE) shock to equivalent per cent], a one per cent appreciation of the exchange rate leads to a fall in headline inflation (core inflation) by 12 basis points (bps) (9 bps) in the first quarter itself²⁰; a one per cent increase in output pushes up headline inflation (core inflation) by 27 bps (28 bps) accumulated over the first two quarters, with the peak impact of 22 bps (18 bps) in the second quarter; while the impact of policy rate changes on inflation lasts longer – a one per cent increase in interest rate results in a fall in headline inflation (core inflation) by 15 bps (16 bps) in the second quarter and a cumulative fall of 50 bps (35 bps) over a span of 3 years (Appendix Table A5). The IRFs also indicate that the impact of an interest rate shock on inflation is highly persistent as compared to the exchange rate shock and output shock.²¹ Further, in terms of the channel via which policy rate shock impacts inflation, the IRFs suggest that the impact is via output, where a positive policy rate shock leads to a fall in output (Appendix Charts A.1 and A.2)²².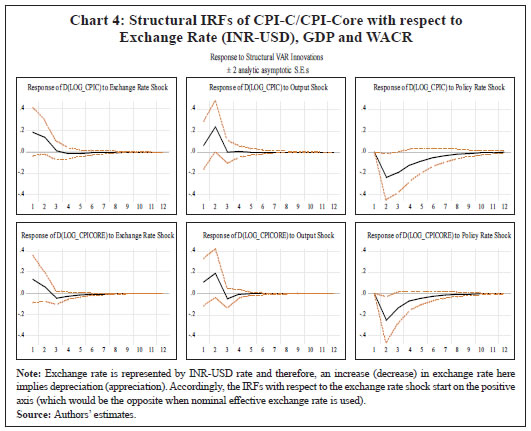

In order to quantify the relative importance of various shocks in explaining the fluctuations in inflation, a variance decomposition analysis was conducted. The results show that the fluctuations in inflation is explained mostly by its own shock. Among the other shocks, the policy rate shock is most important explaining about 7-9 per cent of the variance in inflation over the medium term, as compared to about 2-4 per cent in case of exchange rate and output. Thus, the variance decomposition analysis along with impulse response functions clearly point out the significance of policy rate shock over exchange rate and output shocks for both headline inflation and core inflation in India (Appendix Table A6).

IV.3 Phillips Curve (PC) Based Models

In this section, inflation dynamics is modelled in three ways: the backward-looking triangle model of Gordon (1998); a purely forward-looking NKPC; and a hybrid NKPC which incorporates forward and backward-looking components similar to Gali and Gertler (1999), Patra and Kapur (2012) and Patra, et al. (2014). More precisely, we estimate the following specifications: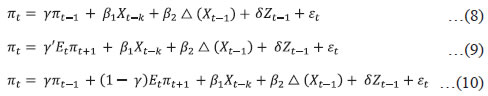

where, π_t is a measure of inflation, X_t is a measure of economic activity represented by output gap [(actual output minus potential output²³/potential output)*100], Δ stands for first difference, and Z_t is a vector of supply side factors; E_tπ_t+1 is the expected future inflation and ε_t is the white noise term (refer to Appendix Table A1a for a detailed description of variables). In equation (10), the coefficients of the inflation terms on the right-hand side are restricted to sum up to unity²⁴, implying the existence of a vertical long-run Phillips curve. All variables, except minimum support prices (MSP) and absolute rainfall deviation from LPA (part of the Z vector), are deseasonalised using Census X-13ARIMA. The presence of unit roots in the variables is tested by employing the augmented Dickey-Fuller test and the test results are presented in the Appendix Table A1b. The difference between the PC specifications in (8), (9) and (10) and the standard ones generally found in extant literature in the Indian context is the presence of the additional term Δ X_t-1 – change in output gap – which is included to capture the possibility of speed limit effects (Fisher, Mahadeva and Whitley, 1997; Gruen, Pagan and Thompson, 1999; Malikane, 2014). The speed limit gets its name from the suggestion that more rapid changes in economic activity may cause larger changes in the inflation rate for a given level of the economic activity (Fuhrer, 1995). The coefficients, β₁ and β₂, therefore provide measures of the flexibility in price adjustment.

Equations (8), (9) and (10) are estimated on quarterly data for the sample period 1996-97:Q1 to 2017-18:Q3 with q-o-q change in headline CPI as well as its major components – core, food and fuel – as dependent variables, using OLS method. Even though PC estimation is typically undertaken using headline or core inflation as the inflation metric, we delve into other major sub-components (food and fuel) for two reasons: first, to understand the drivers of sub-component level inflation dynamics; and second, to generate inflation forecasts from the indirect approach to compare with aggregate level inflation forecast, given the focus of the paper in generating inflation forecasts while capturing the changes in the inflation process. Furthermore, the final form of the equations is derived by starting with a general form with several lags of the output gap and choosing an appropriate model based on the significance of relevant coefficients and overall fit. The results are given in Tables 4, 5, 6 and 7, respectively.

Two variables are used to capture inflation expectations E_tπ_t+1 – the lead q-o-q change in headline CPI (in specification 2) and the lagged headline trend²⁵ (q-o-q) (in specifications 3 and 4) in Table 4. Trend headline inflation can be used as a proxy for expected inflation: (i) as inflation outcome is expected to converge to its trend after the shocks to inflation die out (Behera and Patra, 2020) and (ii) as a substantial portion of observed inflation persistence can be attributed to variation in trend inflation, which in turn is related to changes in monetary regimes (Garnier et al., 2015). Moreover, there was no unique inflation target for the whole sample period (there was a change in the inflation metric for policy from WPI to CPI with the adoption of FIT) which could be used as a proxy for inflation expectations. As can be observed, the leads and lags of price changes are generally significant. The coefficient of lagged headline CPI trend²⁶ is greater compared to lag of headline CPI q-o-q change (Table 4, specification 4), indicating its relative importance in determining inflation dynamics in India. The coefficients of the measure of economic activity – real output gap (7 quarters before) and the change in real output gap (1 quarter before) – are both positive and significant in all the specifications suggesting that demand factors play an important role in determining inflation in India. In other words, inflation depends as much on the change in output gap as on the level implying the presence of speed limit effects. However, the less than proportional impact of output gap on inflation (the lower coefficients) indicates lower degree of flexibility in price adjustment. Other variables that affect headline inflation are MSP, exchange rate and global non-fuel inflation.

Similar to the headline specification, E_tπ_t+1 in the case of core is captured by two variables – lead core q-o-q inflation (specification 2 in table 5) and lagged q-o-q inflation trend derived from headline (specifications 3 and 4). The lags and leads of price changes are significant here too. Besides, the coefficient of lagged headline trend is greater compared to lag of core q-o-q inflation (Table 5, specification 4) as was the case in headline. The coefficients of the level as well as change in the output gap are statistically significant and positive, corroborating the speed limit effects.

Food inflation is modelled in a similar fashion except that it leaves out the output gap variable, as food prices are determined more by supply side factors, given the broadly inelastic nature of food demand²⁸. MSP and rainfall deviation influence food inflation significantly and positively, apart from the lags of inflation. Once again, the lagged headline CPI trend is highly significant, and the magnitude of its coefficient is comparatively higher (Table 6).

Analogously, output gap variables are omitted in the case of fuel inflation as well. The results show that fuel inflation (q-o-q change) is significantly and positively influenced by crude oil inflation. Moreover, identical inferences can be made with regard to lagged headline CPI trend (Table 7).

The Reserve Bank has been collecting 3-months ahead and 1-year ahead inflation expectations of households through quarterly surveys since 2005. Similar to the analysis undertaken in Pattanaik, et al. (2019), we use these survey-based inflation expectations in an NKPC framework for a truncated sample period (and find the results to be qualitatively similar to that of the longer time period discussed in this section (Appendix Table A7) – inflation expectations (both 3-months and 1-year ahead) and output gap are signficant in determining inflation. These results are also in line with Pattanaik, et al. (2019). As a robustness check, these specifications were estimated using IV-GMM as well, and the results were found to be broadly similar (Appendix Tables A8 and A9).

Section V
Evaluating Forecasting Performance

Given the objective of this paper, an evaluation of the forecasting performance is done based on the root mean square errors (RMSEs) and mean absolute errors (MAEs) calculated by comparing the derived y-o-y inflation forecasts generated from these alternative models discussed in section IV with the actual y-o-y inflation.²⁹ Additionally, in line with the literature, we also provide forecasts generated from a random walk model as a benchmark³⁰. We do not go into forecasting inflation at a disaggregated level in the case of SVAR because these models are generally backed by economic theories and linkages that largely work at the macro-level. Moreover, literature also tends to use SVAR models more on validating and establishing larger macroeconomic theories.

In the case of PC models, headline and core inflation forecasts are based on specifications (1), (3) and (4) in Tables 4 and 5 – i.e., we do not employ specification 2 in which inflation expectations are captured through lead headline (core) inflation, as it is useful for modelling but not amenable for out-of-sample forecasting. As discussed earlier, a key objective here is to evaluate the merit of a disaggregated approach; we, therefore, compare the forecasts of headline inflation obtained directly and indirectly (a weighted average³¹ of the forecasts of the three sub-components – core, food and fuel – based on their fixed weights in the CPI-C). Forecast periods are restricted to 2017-18:Q4 to 2019-20:Q4 (9 quarters) for one-period ahead and 2018-19:Q3 to 2019-20:Q4 (6 quarters) for four-periods ahead inflation forecasts to allow forecast comparison over a reasonably long period.

The results indicate that SARIMA outperforms both SVAR and PC models in one period ahead headline forecasts, reflecting gains from flexibility as there are no restrictions (unlike the economic models) to capture the dynamic properties (Litterman, 1986; Stockton and Glassman, 1987). Secondly, in the case of one-period ahead ARIMA forecasting, direct forecasts perform better than indirect ones (sum of component forecasts), indicating that noise associated with volatile food and fuel groups plausibly contaminates the aggregation of forecasts (Table 8). This is in line with the findings of Pratap and Sengupta (2019) for India. Along similar lines, many other studies have concluded that disaggregation does not necessarily imply forecast improvement (Benalal, Diaz del Hoyo, Landau, Roma and Skudelny, 2004; Hubrich, 2005; Cushing, 2014). Finally, while a simple ARIMA on core is better, SARIMA models are better in the case of headline primarily indicating the existence of seasonality in food prices that is captured in headline inflation.

An assessment of four-periods ahead forecasts, however, suggests that the PC-based models (NKPC and hybrid NKPC) perform better than ARIMA/SARIMA models in the case of CPI core; in the case of headline, NKPC and hybrid NKPC outperform every model apart from SARIMA under direct approach (Table 9). Although SVAR model may be capturing the structural dynamics factoring in the role of policy variable, it falls behind PC models in forecasting inflation, which better captures the role of expectations in determining the inflation dynamics in India.

Furthermore, we employ a formal test for comparing forecast accuracy – the Diebold-Mariano (DM) test (Diebold and Mariano, 1995). The null hypothesis of the DM test is that the forecast accuracy of any given two models is equal. We find that direct forecast outperforms the indirect forecast in the case of univariate models both for one-quarter and four-quarters ahead horizons; while in the case of PC-based models, indirect forecasts are generally better compared to direct forecasts³².

These findings indicate that apart from aggregate forecast, disaggregated forecasts may also be useful from the perspective of four-quarters ahead inflation forecasting under different PC models, which better capture the varying properties of the data generating processes of the sub-components of CPI-C in India, which is not possible to capture simply by its own past as in ARIMA models. However, over one-quarter ahead horizon, inflation model based on the behaviour of past inflation alone produces the best forecast. On the other hand, despite poor performance of SVAR models in forecasting, impulse-responses from these models provide useful insights in identifying the direction of linkages and the impact of shocks, which are important in policy analysis and therefore, should be a part of any modelling and forecasting exercise of inflation.

Section VI
Conclusion

Under a flexible inflation targeting monetary policy framework, inflation forecast acts as the intermediate target. Therefore, generating accurate, reliable and unbiased inflation forecasts for the conduct of monetary policy assumes significance. Forecast accuracy helps in the optimal conduct of monetary policy and thereby promotes policy credibility.

This paper models and forecasts CPI inflation using both univariate and multivariate models following two approaches – direct (based on aggregate data) and indirect (based on disaggregate data, i.e., major components of CPI, which are then combined). It corroborates the existence of a PC relationship in India and finds that the dynamics of sub-components of CPI-C are different. While output gap and exchange rate affect core inflation, changes in MSP and rainfall deviation influence food inflation. Fuel inflation is mainly determined by international crude oil prices. Notwithstanding the varying dynamics at the disaggregated level, forecasts generated using the indirect approach do not perform as well as the univariate forecasts at the aggregate level. Furthermore, simple univariate models produce better forecasts compared to structural multivariate models for the one-quarter ahead forecast horizon.

For four-quarters ahead forecasts horizon, however, the PC-based models outperform others in the case of CPI core; in the case of headline, they outperform every model apart from SARIMA under direct approach. Further, PC-based forecasts generated via the indirect approach is better than those generated through the direct approach, indicating that disaggregated level dynamics of inflation could also be useful for generating inflation projections in India. The question on suitability of direct versus indirect forecasts, thus, crucially depends on the forecast horizon and the underlying model. SVAR models, despite having poor forecast performance, provide valuable insights for evaluating the impact of shocks, which are useful from the perspective of policy analysis. As a way forward, inflation forecasting models based on time-varying parameter VAR combined with stochastic volatility may be considered to take into account the changing inflation dynamics over time driven by both structural changes taking place in the economy and shifts in policy regimes.

References

Anand, R., Kumar, N., & Tulin, V. (2016). Understanding India’s food Inflation: The role of demand and supply factors. IMF Working Paper WP/16/2.

Ang, A., Bekaert, G., & Wei., M. (2007). Do macro variables, asset markets, or surveys forecast inflation better?. Journal of Monetary Economics, 54, 1163-1212.

Ascari, G., & Sbordone, A. M. (2014). The macroeconomics of trend inflation. Journal of Economic Literature, 52(3), 679-739.

Atkeson, A., & Ohanian, L. (2001). Are Phillips curves useful for forecasting inflation? Quarterly Review of Federal Reserve Bank of Minneapolis, 25, 2-11.

Ball, L., Chari, A., & Mishra, P. (2016). Understanding Inflation in India. NBER Working Paper Series, No. w22948.

Bańbura, M., Giannone, D., & Reichlin, L. (2010). Large Bayesian VARs. Journal of Applied Econometrics, 25(1), 71-92.

Barnett, W. A., Bhadury, S. S., & Ghosh, T. (2016). An SVAR approach to evaluation of monetary policy in India: Solution to the exchange rate puzzles in an open economy. Open Economies Review, 27(5), 871-893.

Behera, H. K., & Patra, M. D. (2020). Measuring trend inflation in India. RBI Working Paper Series: 15/2020.

Behera, H., Wahi, G., & Kapur, M. (2017). Phillips Curve relationship in India: Evidence from state-level analysis. RBI Working Paper Series: 08/2017.

Benes, J., Clinton, K., George, A. T., John, J., Kamenik, O., Laxton, D., .. Zhang, F. (2016). Inflation-forecast targetig for India: An outline of the analytical framework. RBI Working Paper Series: 07/2016.

Bhattacharya, R., Patnaik, I., & Shah, A. (2008). Exchange rate pass-through in India. New Delhi: National Institute of Public Finance and Policy.

Blanchard, O., Cerutti, E., & Summers., L. (2015). Inflation and activity–two explorations and their monetary policy implications. National Bureau of Economic Research, No. w21726.

Blinder, A. S. (2018). Is the Phillips curve dead? And other questions for the Fed. Wall Street Journal, May 3.

Box, G., & Jenkins, G. (1976). Time Series Analysis: Forecasting and Control. Holden Day: San Francisco.

Brockwell, P., & Davis, R. (1991). Time Series: Theory and Methods. New York: Springer, 2nd edition.

Burnham, K. P., & Anderson, D. R. (2004). Multimodel inference: understanding AIC and BIC in model selection. Sociological methods & research, 33(2), 261-304.

Canova, F. (2011). Methods for applied macroeconomic research. Princeton university press.

Chand, R. (2010). Understanding the nature and causes of food inflation. Economic and Political Weekly, XLV (9), 10-13.

Chinoy, S. Z., Kumar, P., & Mishra, P. (2016). What is responsible for India’s sharp disinflation?. In Monetary Policy in India (pp. 425-452). Springer, New Delhi.

Christiano, L. J., Eichenbaum, M., & Evans, C. L. (1999). Monetary policy shocks: What have we learned and to what end?. Handbook of macroeconomics, 1, 65-148.

Coibion, O., & Gorodnichenko, Y. (2015). Is the Phillips curve alive and well after all? Inflation expectations and the missing disinflation. American Economic Journal: Macroeconomics, 7(1),197-232.

Cushing, S. K. (2014). Does using disaggregate components help in producing better forecasts for aggregate inflation. Journal of Economics and Development Studies, 2(2), 527-546.

Das, S. (2020). Seven Ages of India’s Monetary Policy. Address delivered at the St. Stephen’s College, University of Delhi on January 24, 2020.

Dees, S., Pesaran, M. H., Smith, L. V., & Smith, R. P. (2009). Identification of new Keynesian Phillips curves from a global perspective. Journal of Money, Credit and Banking, 41(7), 1481-1502.

Depalo, D. (2009). A seasonal unit-root test with Stata. The Stata Journal, 9(3), 422–438.

Dholakia, R. H., & Kandiyala, V. S. (2018). Changing dynamics of inflation in India. Economic and Political Weekly, 65-73.

Diebold, F. M., & Mariano, R. (1995). Comparing predictive accuracy. Journal of Business & economic statistics, 13(3).

Dua, P., & Gaur, U. (2009). Determination of inflation in an open economy phillips curve framework: The case of developed and developing asian countries. Working paper 178, Centre for Development Economics; Delhi School of Economics.

Duncan, R., & Martínez-García, E. (2015). Forecasting local inflation with global inflation: When economic theory meets the facts. Globalization and Monetary Policy Institute Working Paper, (235).

Duncan and Martínez-García. (2019). New perspectives on forecasting inflation in emerging market economies: An empirical assessment. International Journal of Forecasting, 35(3), 1008-1031.

Eichenbaum, M., & Evans, C. L. (1995). Some empirical evidence on the effects of shocks to monetary policy on exchange rates. The Quarterly Journal of Economics, 110(4), 975-1009.

Fisher, P. G., Mahadeva, L., & Whitley., J. D. (1997). The output gap and inflation–Experience at the Bank of England. BIS Conference Papers, Vol. 4.

Fuhrer, J. C. (1995). The Phillips curve is alive and well. New England Economic Review, 41-57.

Gali, J., & Gertler, M. (1999). Inflation dynamics: A structural econometric analysis. Journal of Monetary Economics, 44(2), 195-222.

Gali, J., Gertler, M., & Lopez-Salido, D. (2005). Robustness of the estimates of the hybrid New Keynesian Phillips curve. Journal of Monetary Economics, 52(6), 1107–1118.

Garnier, C., Mertens, E., & Nelson, E. (2015). Trend inflation in Advanced Economies. International Journal of Central Banking, 11(4), 65-136.

Gómez, V., & Maravall, A. (1998). Automatic modelling methods for univariate. Banco de España Working Paper No. 9808.

Gordon, R. J. (1998). Foundations of the Goldilocks economy: supply shocks and the time-varying NAIRU. Brookings Papers on Economic Activity, 1998(2), 297-346.

Goyal, A., & Parab, P. (2019). Modelling heterogeneity and rationality of inflation expectations across indian households. IGIDR Working Paper WP-2019-002.

Goyal, A., & Pujari, A. K. (2005). Analysing Core Inflation in India: A Structural VAR Approach. Retrieved from https://mpra.ub.uni-muenchen.de/67105/1/MPRA_paper_67105.pdf

Gruen, D., Pagan, A., & Thompson., C. (1999). The phillips curve in Australia. Journal of Monetary Economics, 44(2), 223-258.

Hendry, D. F., & Hubrich, K. (2006). Forecasting economic aggregates by disaggregates. ECB Working Paper Series (No. 589).

Hubrich, K. (2005). Forecasting euro area inflation: Does aggregating forecasts by HICP component improve forecast accuracy? European Central Bank, Research Department, 21(1), 119– 136.

Huwiler, M., & Kaufmann, D. (2013). Combining disaggregate forecasts for inflation: The SNB’s ARIMA model. Swiss National Bank Economic Studies, (7).

IMF. (2017). Quarterly National Accounts Manual: Chapter 7 - Seasonal Adjustment.

Iyer, T., & Gupta, A. S. (2019). Quarterly forecasting model for india’s economic growth: Bayesian Vector Autoregression Approach. Asian Development Bank Economics Working Paper Series, (573).

John, J., Singh, S., & Kapur, M. (2020). Inflation forecast combinations – The Indian experience. RBI Working Paper Series: 11/2020.

Kabukçuoğlu, A., & Martínez-García, E. (2018). Inflation as a global phenomenon—Some implications for inflation modeling and forecasting. Journal of Economic Dynamics and Control, 87, 46-73.

Kapur, M. (2013). Revisiting the Phillips curve for India and inflation forecasting. Journal of Asian Economics, 25, 17-27.

Kapur, M., & Patra, M. D. (2000). The Price of Low Inflation. Reserve Bank of India Occasional Papers, 21(2), 191-234.

Kim, S., & Roubini, N. (2000). Exchange rate anomalies in the industrial countries: A solution with a structural VAR approach. Journal of Monetary economics, 45(3), 561-586.

Litterman, R. B. (1986). Forecasting with Bayesian vector autoregressions—five years of experience. Journal of Business & Economic Statistics, 4(1), 25-38.

Malikane, C. (2014 ). A new Keynesian triangle Phillips curve. Economic Modelling 43, 247-255.

Mandalinci, Z. (2017). Forecasting inflation in emerging markets: An evaluation of alternative models. International Journal of Forecasting, 33(4), 1082-1104.

Mathai, K. (2009). Back to basics: What is monetary policy?. Finance & Development, 46(003).

Mazumder, S. (2011). The stability of the Phillips curve in India: Does the Lucas critique apply? Journal of Asian Economics, 22(6), 528-539.

Meyler, A., Kenny, G., & Quinn, T. (1998). Forecasting irish inflation using ARIMA models. Central Bank and Financial Services Authority of Ireland Technical Paper Series, 1-48.

Mishra, A., & Mishra, V. (2012). Evaluating inflation targeting as a monetary policy objective for India. Economic Modelling, 29(4), 1053–1063.

Mohanty, D. (2014). Why is recent food inflation in India so persistent? Annual Lalit Doshi Memorial Lecture, St. Xavier’s College, Mumbai.

Mohanty, D., & John, J. (2015). Determinants of inflation in India. Journal of Asian Economics, 36, 86-96.

Nason, J. M., & Smith, G. W. (2008). Identifying the new Keynesian Phillips curve. Journal of Applied Econometrics, 23(5), 525-551.

Benalal, N., Diaz del Hoyo, J. L., Landau, B., Roma, M., & Skudelny, F. (2004). To aggregate or not to aggregate? Euro area inflation forecasting. Euro Area Inflation Forecasting (July 2004).

Ouliaris, S., Pagan, A., & Restrepo, J. (2016). Quantitative macroeconomic modeling with structural vector autoregressions–an Eviews implementation. IHS Global, 13.

Özmen, M., & ŞANLI, S. (2017). Detecting the best seasonal Arima forecasting model for monthly inflation rates in Turkey. Dokuz Eylül Üniversitesi İktisadi İdari Bilimler Fakültesi Dergisi, 32(2), 143-182.

Pankratz, A. (1983). Forecasting with Univariate Box-Jenkins Models: Concepts and Cases. John Wily & Sons.

Patra, M. D., & Kapur, M. (2012). A monetary policy model for India. Macroeconomics and finance in emerging market economies, 5(1), 18-41.

Patra, M. D., & Ray, P. (2010). Inflation expectations and monetary policy in India: An Empirical Exploration. IMF Working Paper (WP/10/84).

Patra, M. D., Behera, H., & John, J. (2021). Is the Phillips curve in India dead, inert and stirring to life or alive and well? RBI Bulletin, November, 63-75.

Patra, M. D., Khundrakpam, J. K., & George, A. T. (2014). Post-Global crisis inflation dynamics in India: What has changed? In S. Shah, B. Bosworth, & A. Panagariya, India Policy Forum 2013-14 (pp. 117-191). New Delhi; Washington DC: Sage publications.

Patra, M.D., Khundrakpam J. K., and John, J. (2018). Non-linear, asymmetric and time-varying exchange rate pass-through: Recent evidence from India. RBI Working Paper Series: 02/2018.

Pattanaik, S., Muduli, S., & Ray, S. (2019). Inflation expectations of households: Do they influence wage-price dynamics in India? RBI Working Paper Series: 01/2019.

Paul, B. P. (2009). In search of the Phillips curve for India. Journal of Asian Economics, 20(4), 479–488.

Phillips, A. W. (1958). The relation between unemployment and the rate of change of money wage rates in the United Kingdom, 1861-1957. Economica, 25(100), 283-299.

Pincheira, P., & Medel, C. (2012). Forecasting inflation with a random walk. Bank of Chile Working Paper No. 669.

Pratap, B., & Sengupta, S. (2019). Macroeconomic forecasting in india:does machine learning hold the key to better forecasts? RBI Working Paper Series: 04/2019.

Raj, J., Kapur, M., George, A., Wahi, G., & Kumar, P. (2019). Inflation forecasts: Recent experience in India and a cross-country assessment. The Reserve Bank of India Mint Street Memo No. 19, May.

RBI. (2021). Report on Currency and Finance 2020-21: Reviewing the Monetary Policy Framework.

Saz, G. (2011). The efficacy of SARIMA models for forecasting inflation rates in developing countries: The case for Turkey. International Research Journal of Finance and Economics, 62, 111-142.

Sharma, S., & Padhi, I. (2020). An alternative measure of economic slack to forecast core inflation. Reserve Bank of India Occasional Papers, 41(2).

Singh, B. K., Kanakaraj, A., & Sridevi, T. (2011). Revisiting the empirical existence of the Phillips curve for India. Journal of Asian Economics, 22(3), 247-258.

Sonna, T., Joshi, H., Sebastian, A., & Sharma, U. (2014). Analytics of food inflation in India. RBI Working Paper Series: 10/2014.

Srinivasan, N., Mahambare, V., & Ramachandran, M. (2006). Modelling inflation in India: A critique of the structuralist approach. Journal of Quantitative Economics, 4(2), 45-58.

Srivastava, S. K. (2016). Short run forecast of food inflation using ARIMA: A combination approach. In Analytical Techniques for Decision Making in Agriculture. (pp. 82-92). Daya Publishing House.

Stock, J. H., & Watson, M. M. (2008). Phillips curve inflation forecasts. NBER Working Paper (w14322).

Stock, J. H., & Watson, M. W. (2007). Why has US inflation become harder to forecast?. Journal of Money, Credit and Banking, 39, 3-33.

Stock, J. H., & Watson, M. W. (2010). Modeling inflation after the crisis. NBER Working Paper, No. w16488.

Stockton, D. J., & Glassman, J. E. (1987). An evaluation of the forecast performance of alternative models of inflation. The review of economics and statistics, 69(1), 108-117.

Uhlig, H. (2005). What are the effects of monetary policy on output? Results from an agnostic identification procedure. Journal of Monetary Economics, 52(2), 381-419.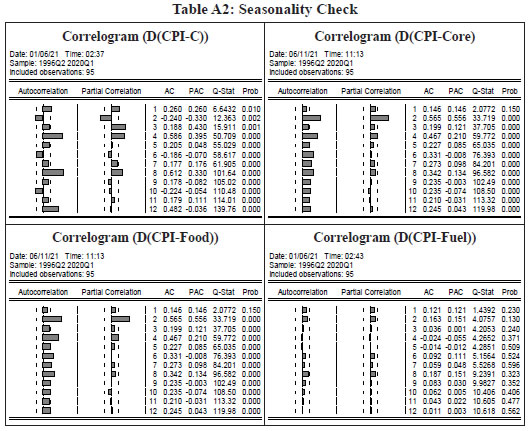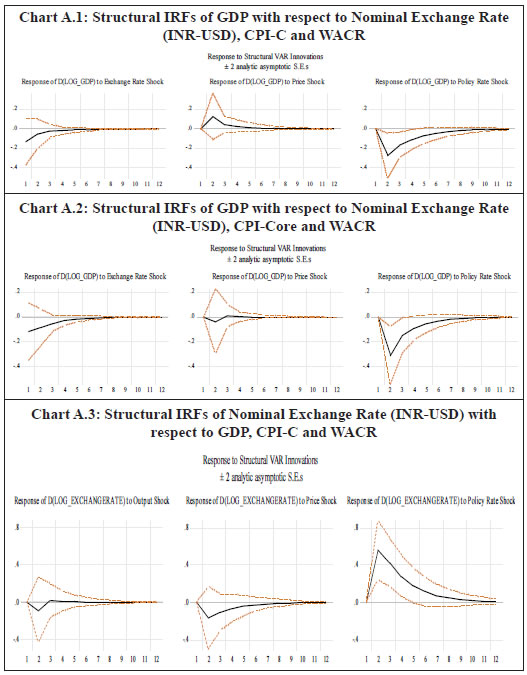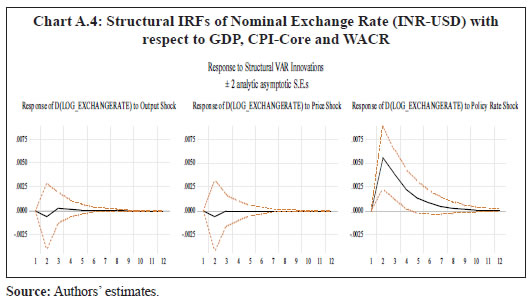

Appendix

^* Jibin Jose, Himani Shekhar and Vimal Kishore are Managers; Sujata Kundu is Assistant Adviser and Binod B. Bhoi is Director in the Department of Economic and Policy Research, Reserve Bank of India. An earlier version of this paper was presented in DEPR colloquium on June 28, 2021. Comments from Prof. Rudrani Bhattacharya, NIPFP and an anonymous reviewer are gratefully acknowledged. The views expressed in the paper are those of the authors and do not represent the views of the Reserve Bank of India. Corresponding author email: jibinjose@rbi.org.in

¹ On August 5, 2016, the Government of India set out the inflation target for the first time for a period of five years up to March 31, 2021. The target was renewed for a further period of five years from April 1, 2021 to March 31, 2026.

² QPM is a forward-looking open economy calibrated gap model broadly following a theoretical framework founded on New Keynesian principles embedding key India-specific features like behaviour of different inflation components and their interlinkages as well as monetary-fiscal interactions.

³ Data on CPI-C from January 2011 correspond to the base year 2012. Data prior to that correspond to CPI for Industrial Workers (CPI-IW) with base year 2001 rebased to 2012.

⁴ It is measured by the year-on-year per cent change in the all-India CPI-C series with base year 2012 released by the National Statistical Office (NSO), Ministry of Statistics and Programme Implementation (MoSPI), Government of India. Prior to 2011, CPI-IW rebased series is used.

⁵ The weights correspond to the current base year (2012=100) of CPI-C.

⁶ Core inflation is generally calculated by excluding the volatile components/sub-groups in the CPI. Since, food and fuel groups are largely the broader volatile components in the consumption basket as their prices are more often driven by supply shocks, excluding them from the headline index is considered as one of the several possible measures of core inflation. By its very construct, therefore, core inflation is the least volatile among the three major groups of CPI-C.

⁷ Multiple indicators approach was adopted in April 1998 (in place of monetary targeting) under which besides monetary aggregates, a host of forward-looking indicators such as credit, output, inflation, trade, capital flows, exchange rate, returns in different markets and fiscal performance constituted the basis of information set used for monetary policy formulation (Das, 2020). In the post-global financial crisis period, however, the credibility of this framework came under question as persistently high inflation and weakening growth began to co-exist. This paved way for transition to FIT with the Expert Committee set up by RBI to revise and strengthen the monetary policy framework recommending headline CPI inflation to be the nominal anchor for monetary policy in January 2014. Consequently, RBI adopted a self-imposed glide path to bring inflation down sequentially, leading up to the Monetary Policy Framework Agreement (MPFA) signed in February 2015 and formal adoption of FIT with the amendment to the RBI Act in May 2016.

⁸ Unlike Behera and Patra (2020), the focus of this paper is not on accurate measurement of trend inflation, which is crucial for setting the inflation target, but on forecasting inflation and therefore, we have used two-sided HP filter for deriving a gauge on the trend component for its use in the PC based forecasting models.

⁹ In India, CPI-C (Base: 2012=100) is constructed following a bottom-up approach by first compiling price index at the item level and then at the sub-group/group level for both rural and urban areas across states, which are then combined using respective fixed weights.

¹⁰ The idea that there is a trade-off between rates of inflation and unemployment – the formal empirical evidence for which was originally provided by Phillips (1958) using data on wage inflation in the United Kingdom – has occupied the centre stage of policy decisions and debates in this sphere over the last sixty years.

¹¹ With the exception of Dua and Gaur (2009) and Singh, Kanakaraj and Sridevi (2011).

¹² Sample period of estimation for various models is restricted to 2017-18Q3 to facilitate a comparison of out of sample forecasts of relatively longer period for model evaluation.

¹³ ARIMAX models have not been attempted here as we wanted the simplest univariate model as a benchmark. Other exogenous variables are taken into account in the SVAR and PC based models.

¹⁴ All specifications are obtained using logarithmic transformed data.

¹⁵ Results of seasonal unit root test (HEGY test) indicate seasonal differencing is not needed.

¹⁶ The month-wise average WACR is used to obtain quarterly averages.

¹⁷ Moreover, a set of dummy variables to capture exchange rate fluctuations during the Asian financial crisis of 1997-98, global financial crisis of 2007-08, food price upsurge in 2010-11 and taper tantrum episode of 2013-14 were also incorporated as exogenous variables in the model to enhance model performance.

¹⁸ Before going into SVAR, the three non-stationary variables CPI-C/CPI-Core; INR-USD; GDP were checked for the existence of any long-run cointegrating relationship and the results did not pass the Johansen Cointegration Test. It was not explored further given the objective of the paper on forecasting.

¹⁹ An alternate specification with output gap instead of real GDP was also attempted. However, it did not produce statistically significant results.

²⁰ These estimates are in line with the findings in the literature in India, that show a cumulative pass through of exchange rate impact on headline inflation in the range of 10-15 per cent over a period of 4-5 months (Bhattacharya et al. 2008; Patra et al. 2018; RBI, 2021).

²¹ IRFs based on the applied SVAR framework (standard monetary VAR in line with the interest rate rule in which the monetary authority responds to the current level of output and/or output gap and inflation, augmented with an exchange rate variable) generally display impulse response anomalies – ‘price puzzle’ and ‘exchange rate puzzle’ (Barnett et al. 2015; Ouliaris et al., 2016; Goyal and Parab, 2019). Price puzzle is the one in which monetary policy shocks have a positive effect on inflation instead of a negative effect, while the exchange rate puzzle is where a monetary policy shock that raises interest rates depreciates rather than appreciates a currency. In the Indian context, Goyal and Parab (2019) find evidence of price puzzle. Literature provides methods that may eliminate such puzzles, broadly centring around re-specifying the SVAR model in some manner. Some of the methods are: incorporating additional/latent variables into the SVAR framework (such as, global crude oil prices, global commodity prices or any other variable that influence inflation or price-setting mechanism); re-defining the variables (using output gap instead of output); and different model specifications. Our SVAR model also showed both the puzzles. However, the introduction of rainfall deviation and Indian basket crude oil price as exogenous variables in the model helped to eliminate the price puzzle, while the exchange rate puzzle remains (Appendix Charts A.3 and A.4).

²² Among the alternative channels of monetary policy transmission (Mathai, 2009), the SVAR here focuses only on the interest rate channel - a hike in the policy rate raises borrowing costs of consumers and investors and thereby reduces aggregate demand and brings down inflation – in view of the current operating framework of monetary policy in India.

²³ Potential output is measured by the HP filtered trend output.

²⁴ This restriction also implies that inflation is dynamically homogenous.

²⁵ Trend inflation is slow moving and there may not be any difference between its one period lag and lead, and therefore lagged trend is used which facilitates estimation by OLS.

²⁶ ‘Inflation trend’ is constructed by applying the HP filter on the CPI headline q-o-q series and is used to represent trend in case of food, fuel and core inflation.

²⁷ In constrained regressions, a comparable R2 cannot be obtained, and hence not reported.

²⁸ Alternate specifications with output gap (up to four lags) for food inflation were attempted; however, the coefficient turned out to be statistically insignificant and therefore have been dropped from the final set of models.

²⁹ The models are based on log first-differenced quarterly data on CPI with seasonal adjustment in case of SVAR and PC models and without seasonal adjustment in case of ARIMA and SARIMA models. The forecast output is in the form of the respective indices (barring PC-based models where the forecast output is quarter-on-quarter change in the index), which are then used to derive year-on-year (y-o-y) inflation forecasts, and then compared with the actual inflation outcomes to generate the respective model RMSEs.

³⁰ A random walk model, which is defined as a process where the current value of a variable is composed of its past value plus an error term defined as a white noise (π_t =π_t-1 + ε_t), is often used as a common benchmark for forecast evaluation (Raj et al., 2019). Studies have shown that persistent stationary processes may be better predicted by drift less unit-root-based forecasts than by forecasts coming from a model that is correctly specified but that is subject to a higher degree of parameter uncertainty (Pincheira and Medel, 2012). Comparing the forecast performances of various Phillips curve-based inflation models with a random walk model, another study finds that for the US, the random walk forecasts perform better (Atkeson and Ohanian, 2001).

³¹ Weights correspond to the weights of these groups in the CPI-C basket (Core: 47.30 per cent; Food: 45.86 per cent; and Fuel: 6.84 per cent).

³² DM test results imply that in the case of ARIMA and SARIMA models, across both forecast horizons, the null hypothesis of equal forecast accuracy is rejected in favour of direct forecasts. In the case of PC-models, indirect forecasts are better in 4-period ahead forecasts, while the null hypothesis is not rejected in the case of 1-period ahead forecasts.