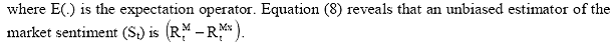IST,
IST,
RBI WPS (DEPR) : 04/2012: Asset Pricing Model for Inefficient Markets: Empirical Evidence from the Indian Market
| RBI Working Paper Series No. 04 Abstract *In the last decade, the efficient market hypothesis and its validity for emerging markets grew as a fertile topic of debate in finance. However, the dilemma of market efficiency still remains intractable. It is more likely that any literature review in respect of market efficiency would produce contradictory results: for a single paper producing empirical evidence supporting the market efficiency, we can perhaps find a contradictory paper which empirically establishes market inefficiency. Paradoxically, popular models in finance developed in 1970s or 1980s were based on the assumption that the market under consideration was efficient. The conventional bond or stock or option pricing models are common examples of this type. In an alternative approach, we have worked out a model which incorporates market sentiments in the domain of the standard rational model of asset pricing. Our model would be well applicable for a ‘less than’ efficient market and, therefore, may be the useful input in investors’ policies. JEL Classification: G12, G14 Key Words: Capital Asset Pricing Model, Arbitrage Pricing Theory, Efficient market hypothesis Theories for the pricing of a bond or a stock or an option were considered by economists as an enormous breakthrough in the history of finance. Their inventors, however, believed that financial markets evolve with some special characteristics: market prices adjust to new information without delay and, as a result, no arbitrage opportunities exist that would allow investors to achieve above-average returns without accepting above-average risk. This hypothesis is associated with the view that price movements approximate those of a random walk. If new information develops randomly, then so will market prices, making the market unpredictable apart from its long-run uptrend. Under such a backdrop, the Geometric Brownian Motion (GBM) process, also called a lognormal growth process, had gained wide acceptance as a valid model for the growth in the price of a stock over time. Most economists in the 1970s and 1980s considered the GBM process or its ancestor, the efficient market hypothesis, the leading principle to understand the basic nature of a financial market and therefore were critical inputs in various asset-pricing models. Black-Scholes option pricing model is a common example of the above type of models. Conversely, Capital Asset Pricing Model (CAPM), or its any modified versions, depend on identifying a “market portfolio” that is mean-variance efficient. Practically, such a portfolio could be any index of an efficient capital market. Thus, a tradition grew according to which it was legitimate to consider any market index as a proxy of such a portfolio. However, prior to the use of the model, the question of the validity of the applicability of efficient market hypothesis to the market under consideration was hardly addressed. Even if such a question is addressed, any literature review in respect of market efficiency would likely to produce contradictory results: for a single paper producing empirical evidences supporting the market efficiency, we can perhaps find a contradictory paper which empirically establishes market inefficiency. These studies are based on statistical tests for market efficiency which can be broadly classified into two categories: one, ‘event studies’ that examine market reactions after major economic events and two, exploring overtime predictability in equity returns. When the outcomes of these tests are indicative of market inefficiency, application of common asset pricing models might result in significant flaws in an institution’s policies. This is so because a common model for pricing stocks or bonds or options is based on the assumption that asset prices follow a martingale process over short horizons as systematic short-run changes in fundamental values is negligible with unpredictable information arrival. For the purpose of avoiding mispricing caused by a standard asset pricing model, several scholars advocate an unconventional approach to asset pricing. One of these approaches might be an unconditional or conditional autoregressive processes which are expected to perform better compared to a standard arbitrage pricing model, particularly when stock returns are predictable through time. Here, the dilemma is that on some occasions, lagged returns cannot explain a major portion of the variation in equity returns. Alternatively, the researcher can select a combination of the market return and lagged returns to develop an empirical model providing a better fit to the equity data. However, critics may question the theoretical justifications of these models. The question is ‘what would be the appropriate asset pricing model for those markets which are not uniformly efficient for all periods?’. The model proposed in present paper might be an answer. It adopted methodologies in the line of Majumder (2006)1: equity price changes due to investors' sentiments (collective) can be modeled and isolated from original equity price movements (or returns). The residual part is the portion of the equity price (or return) that is governed by the factors which caused a systematic change in it. Such prices (or returns) would correspond to a hypothetical efficient stock market and can be used as an effective input in the bond or stock pricing formula. The process of transforming the original market to a hypothetical market, which is relatively efficient, smooths out, at least partially, the abnormal volatility and large autocorrelations often found in the asset return data without changing the properties of the original asset pricing model. The outcome might be a superior alternative to a conventional model in terms of its greater applicability. The rest of the paper is organized as follows. Section II provides the literature review. Section III describes the model. Section IV provides data description and stylized facts. Section V provides empirical findings. Policy implications of the model are given in Section VI and Section VII concludes. Beginning with Sharpe (1964) and Lintner (1965), economists have systematically studied the asset pricing theory or, precisely, the portfolio choice theory of a consumer. Sharpe (1964) and Lintner (1965) introduced the Capital Asset Pricing Model (CAPM) to investigate the relationship between the expected return and the systematic risk. From the day CAPM was developed, it was regarded as one of the primary models to price an equity or a bond portfolio. However, economists of the later generation worked out an Intertemporal Capital Asset Pricing Model (ICAPM) and Arbitrage Pricing Theory (APT) which are more sophisticated in comparison with the original CAPM (e.g. Merton, 1973; Ross, 1976). These models and also models for pricing options as developed by Black and Scholes (1973) effectively predict asset returns for given levels of risks which are useful information to an investor in the case of selecting his portfolio or a banker in the case of monitoring the financial health of a company. Over last four decades, investors, bankers and market researchers used such models to predict asset returns in normal market conditions. The “normal market condition” essentially means equity prices are not driven by any sentiment or stocks are not systematically overvalued or undervalued by the market players. In such circumstances, markets act like efficient markets (e.g. Fama, 1970; Fama, 1991; Fama, 1998). But, an anomaly arises when such conditions are not applicable for a capital market. For example, Chan, Gup & Pan (1997), Rubinstein (2001), Malkiel (2003 & 2005) and many others provided empirical evidences in favour of market efficiency. Conversely, we can provide references of studies by Fama and French (1988), Poterba and Summers (1988), Lo and MacKinlay (1988), Cutler, Poterba and Summers (1989) and Jegadeesh (1990) whose findings are indicative of a market inefficiency. Over the past 20 years, several scholars documented overtime predictability in stock returns in different set of markets. For developed markets, we can quote examples of Blandon (2007), Jegadeesh and Titman (1993), Gregoriou, Hunter and Wu (2009), Avramov, Chordia, Goyal (2006), Pesaran and Timmermann (1995) and Kramer (1998) who empirically established the existence of autocorrelation in equity returns for daily, weekly and monthly returns. Chen, Su, Huang (2008) observed positive autocorrelation in US stock market even in shorter horizon returns than the daily returns. Similar results for emerging markets were observed by Chang, Lima and Tabak (2004), Mollah (2007) and Harvey (1995a and 1995b). Empirical results by these authors established that in many occasions past returns contain additional information about expected stock returns. In those circumstances, it is expected that an unconditional or a conditional autoregressive process performs better compared to a standard APT model. This might be the motivation of Conrad and Kaul (1988), LeBaron (1992) and Koutmos (1997) to model a stock-return as a suitable autoregressive process. However, many scholars observed that return autocorrelations are sample dependent and may exhibit sign reversals (e.g. Chan, 1993, p. 1223; Knif, Pynnonen & Luoma, 1996, p. 60; McKenzie and Faff, 2005). Alternatively, the combination of the market return and the lagged returns might develop an empirical model providing a better fit to the equity data. However, critics may question about theoretical justifications of this kind of models. The autocorrelations in equity returns might be an outcome of the scenario when an individual investor’s investment decision is atleast partially guided by investors’ sentiments (e.g. Barberis, Shleifer & Vishny, 1998; Majumder, 2006). We generally observe that investors’ sentiments peak or trough when the market experiences extreme events. The effects gradually reduce with a reduction in volatility and finally reach normal levels with low volatility. Consequently, it can be argued that the equity price today is an outcome of the combined effect of news/information released in the market and subsequent sentiments cultivated by them. Essentially, any analysis on the equity market remains incomplete if the effect of any one of the above two factors is neglected. Because of this feature of the equity market, it is generally observed that equity prices do adjust to new information, but the adjustment process is not instantaneous. Consequently, underreactions and overreactions by investors are common (e.g. Chopra, Lakonishok and Ritter, 1992; Barberis, Shleifer and Vishny, 1998). In the case of such underreactions or overreactions, the equity price gradually adjusts to its fair value after a certain period. Gradual price adjustments after underreaction induce a positive autocorrelation, a price reversal caused by overreaction induces a negative autocorrelation in equity returns. Essentially, underreactions and overreactions are results of market sentiments that lead all the stocks to move in a particular direction resulting in an equity return to be correlated with itself or to any other stock return. In addition to the above, the occasional exuberance or pessimism by investors to certain information leads the stock return to be more volatile. Even in a developed market like the US, it can be observed that equity returns are more volatile than implied by equity fundamentals (e.g. Shiller, 1981; Leroy and Porter, 1981; and Shiller, 1987). These characteristics of the equity return are even common in an emerging market like India and also the volatility in equity return is higher in the developing world as compared to the developed world (see Parametric Portfolio Associates, 2008). These are the common evidence of inefficiencies in emerging markets as well as developed markets. The standard bond or stock pricing models are not applicable for an inefficient market. In an alternative approach, we have worked out a model which incorporates market sentiments in the domain of the standard rational model of asset pricing. Our model is applicable for a ‘less than’ efficient market and, therefore, may be a useful input in investors’ toolkits. The capital market is composed of a continuum of investors who purchase or sell financial assets in the form of equities. We assume that the market is frictionless. However, the behavior of investors is governed by market sentiments. As an example, post-election uncertainty or uncertainty in policies of newly elected governments often induces a panic among investors which subsequently may lead to a major downfall in equity prices. The stock market crash in India on 17th May 2004 was an example (Majumder, 2006). It was the biggest ever fall at that time in a single day’s trading in the Indian equity market which occurred due to the panic that the newly elected government could halt economic reforms. The outcome, however, was independent of the fundamentals of Indian firms. Thus, any upturn/downturn in equity prices might be a consequence of any of the hundreds of unforeseen events, such as frauds or war or droughts or hikes/fall in oil prices etc. These events are not predictable. All the same, influencing market sentiment they change overall supply/demand conditions and consequently disrupt the stability of markets. While it is impossible to predict ex-ante all of these events causing stock price movements, the common approach to develop an asset pricing model accepted by earlier generation economists include selecting firm-specific and macroeconomic factors which have an influence on general decisions of an investor. These factors are of two kinds: one set of factors is correlated with equity fundamentals and the other set of factors is uncorrelated with them. Ideally, effects of fundamentals on the stock return cause a systematic change in it. This would essentially be the systematic component of the stock return. This component is influenced by factors like the financial health of the firm, implicit market risk and the economy’s position in the business cycle etc. The financial health of a firm can be assessed by some parameters like the firm size, the leverage, earnings-to-price ratios, book-to-market equity ratios etc. These factors are responsible for cross sectional variation in the stock returns. In contrast, nonfundamentals would essentially be the transitory component of the stock return which is influenced by factors like market sentiments and noise. In the short run, the market sentiment influences all the stocks in a specific direction, either upward or downward. The resulting stock returns depart from their fair values. In course of time it reverts to its original position. Therefore, the short-run expectation of the return of a stock depends, with other factors, on the market sentiments. However, in the long run, the market reaches its normal position where the effects of sentiments are zero and, therefore, the expectation would be consistent with fundamentals.
A. The Market Sentiments Our model is based on the basics of isolating effects of non-fundamentals from the equity return. The residual part of which is the component of the equity return governed by the factors which caused a systematic change in it. Therefore, this part can be taken as an input in an asset pricing model. Non-fundamentals would essentially be investors’ sentiments. However, effects of investors’ sentiments are not observable from the market and also never clearly defined in economics literature. According to the theory of capital markets, news/ information released in the market is the driving force behind an investors’ investment decision. However, apart from news/information, an individual investor’s investment decision is also guided by collective beliefs, also termed investors’ sentiments. Investors’ sentiments peak or trough when the market experiences extreme events. We are experienced, in the one extreme, investors’ sentiments render into a panic which may lead a sharp downturn in the market index. In the other extreme, positive sentiments may cause a significant rise in the market index. Therefore, the initial step in modeling market sentiments might be based on the assumption that effects of market sentiment are properly summarized into a diversified market portfolio. However, it is not necessarily implied that sentiments are the only factors behind any ups or downs of market returns. Movements in the market return are essentially due to the combined effects of market fundamentals and collective investors’ sentiments. Consequently, it is not difficult for a researcher to segregate the above two effects by fitting a linear model.
B. The Systematic Component
C. The adjustments, when factors F and S are not uncorrelated
IV. Data Description and Stylized Facts National Stock Exchange (NSE) in India maintains 11 major indices and 14 sectoral indices, details of which are given in the Annex. These indices are computed on a free float-adjusted market capitalization weighted methodology which is a popular approach. They are comparable across sectors and, therefore, used extensively in empirical research. Among these major and sectoral indices compiled by the NSE, six indices are selected for our empirical analysis. These indices are: S&P CNX Nifty (P1), CNX Nifty Junior (P2), S&P CNX Defty (P3), Bank Nifty (P4), CNX Midcap (P5) and CNX Infrastructure (P6)2. Based on these indices, applicability of standard asset pricing models is examined by us for Indian markets. These models have been recognised as useful quantitative tools behind an investor’s asset allocation strategies or in monitoring performances of his existing investments. However, these models are useful to the extent they are supported by empirical regularities observed in market returns. Unfortunately, all conventional forms of these models and their empirical validity have been questioned by several scholars over past twenty years (see Bird, Menzies, Dixon, and Rimmer (2010); Majumder (2011)). This tenet of research was the exploration of certain regularities in market returns which were not the fruit of the standard models. Predominant among these observed empirical phenomena would be the predictability of portfolio returns through time. On many occasions, past returns contain additional information about expected asset returns which lead asset returns to be serially correlated. Serial dependence in portfolio returns is evidence in favour of market inefficiency which is examined by us for Indian markets. This test has been performed separately for the original market and the hypothetical market to show that hypothetical market returns are, in general, not autocorrelated and so meet the prerequisites of applying an asset-pricing model. Prior to manipulating any asset pricing model for predicting equity returns, it is worthwhile to examine whether the capital market is informationally efficient. One effective way to test this might be through investigating serial correlation properties of equity returns. Such test is also useful to examine existence of investors’ sentiment in the equity market. In the present paper, the test is performed on daily portfolio returns in the similar line of Jegadeesh (1990). The particular cross-sectional regression model used in the empirical tests is
Scenarios can be based on a significant market events in the past (a historical scenario) or on a plausible market event that has yet to happen (a hypothetical scenario). A historical scenario is generated from historical data and is used extensively in financial research (BCBS 2009). It involves identifying risk factors based on actual historical events. The basic insight of this method is that the events which happened in reality are plausible to reappear. With this method, the range of observed risk factors changes during a historical episode is applied to the portfolio to get an understanding of the portfolio’s risk in case such a situation recurs (Blaschke, et al., 2001, p. 6). We have identified historical events which caused large movements in equity returns in the Indian markets that include equity market crash in May 2004, May 2006, the recent financial crisis that began since July 2007 and many others. Movements in returns as consequences of these events provide the high volatile scenario and if these consequences are separated from the historical dataset, it gives low to medium volatile scenario. The return distribution of a portfolio under a simulated historical scenario is given by the empirical distribution of past returns on this portfolio. Regression model in the equation (16) has been estimated using daily returns over the period January, 2003 to March, 2009 separately for low to medium volatile scenario and high volatile scenario. Results for the original and the hypothetical market are presented in the table 1 and 2 respectively.
sectional regressions is 0.032; i.e., on average the lagged returns considered here can explain 3.2 percent of the cross-sectional variation in individual security returns. Our results are consistent with the findings of earlier authors (see Kramer, 1998; Blandon, 2007). Contrarily, table 2 indicates that for almost all occations, coefficients for lagged returns are not statistically significant for both the scenarios resulting a very low R2 of regression. Therefore, in general, stock returns in the hypothetical market are not autocorrelated. The results can be verified further by presenting F-statistics under the hypothesis that all slope coefficients are jointly equal to zero. Table 3 indicates that for the original market almost all F statistics are statistically significant at 5% significant level indicating all slope coefficients are not jointly equal to zero. However, results are opposite for the hypothetical market where most of the F statistics are statistically insignificant. The results indicate that the original equity market returns are autocorrelated for at least one lag, however the hypothetical market returns are not so autocorrelated. VI. An optimal allocation of resources - Policy Implications of the model We can quote from Lady Windermere’s Fan by Oscar Wilde, “What is a cynic? A man who knows the price of everything, and the value of nothing”. The observations by the great novelist is appropriate as well for a modern investor who evaluates the value of his investments by using any conventional asset pricing model and subsequently encounters mispricing. Paradoxically, CAPM, APT and their presently available variants might be wonderful advancements in this profession, but one could easily understand that they are not true descriptions of the world around us. These models are based on the basics that past returns do not have memory or predictability power, which is empirically an untenable assumption (see Gregoriou, Hunter and Wu (2009); Mollah (2007); Avramov, Chordia and Goyal (2006)). Thus, a modern investor may not become skeptic when he encounters mispricing. While exploring the causes of this mispricing, Bird, Menzies and Rimmer (2010) asserted that the foundation for this mispricing well encapsulated by the words and irrational exuberance which reflect a period when emotions take over and valuation plays at best a limited role in determining equity prices. Valuation by any existing model would likely produce a suboptimal risk-return relationship which may guide an investor to adopt wrong policies for his new investments or for reallocating his old investments. Such investment strategies, collectively, may also affect the real economy by disrupting the optimal allocation of resources. Conversely, our model provides a direction of incorporating market sentiments in the domain of the standard rational model of asset pricing. The process of transforming the original market to a hypothetical efficient market, described in the preceding section, will smooth out, at least partially, the abnormal volatility and large autocorrelations often found in the asset return data without changing properties of the original asset pricing model. The outcome might be a superior alternative to a conventional model which can be applicable for all sets of markets ranging from an emerging to a developed one. Major policy implications of this generalization of standard asset pricing models inherent in its greater applicability, some of which are specified below:
A generation ago, the efficient market hypothesis was widely accepted by financial economists as a principle to explain the price behavior in a financial market. It was, therefore, the theoretical basis for much of the financial market researches during the 1970s and the 1980s. Among the theories developed at that time, bond, stock and option pricing theories were the leading examples which presumed that the underlying market is informationally efficient. These theories are based on the assumption that asset prices follow a martingale process over short horizon as systematic short-run changes in fundamental values is negligible with unpredictable information arrival. However, these assumptions are not applicable for most of the equity market in the today’s world because it became a stylized phenomenon that daily, weekly and monthly equity returns are over time predictable. In such circumstances, the conventional asset pricing models might be considered as one extreme representation of the reality. Alternatively, the researcher may select a suitable autoregressive model for the equity return which, however, might be the other extreme representation of the reality. This model is applicable when the variation through time in short-horizon expected returns is the leading component of the return variance. Above two approaches are based on mutually conflicting hypothesis and, therefore, each of them is the partial representation of the reality. The present paper argued that the equity price today is an outcome of the combined effect of news/information released in the market and subsequent sentiments cultivated by them. However, the market sentiment is unobservable. At the same time, it can be defined as the stationary departure of the market return from its fair value. This part of the market return is explained by the exuberance or pessimism by investors to certain information. Consequently, any autocorrelation that is observed in the market return might be the result of possible bullish/bearish responses by investors to market information. Against this backdrop, our paper makes following contributions to the conventional economics literature: first, we propose that equity price changes due to investors' sentiments (collective) can be modeled and isolated from original equity price movements (or returns). The residual part is the portion of the equity price (or return) that is governed only by equity-fundamentals and the noise. Therefore, if a hypothetical stock market is constructed using prices (or returns) as that of the residual part, and all other parameters are identical to the original equity market, then such a market must be an efficient market. In that market, investors' sentiments cannot induce investors to systematically overvalue or undervalue a stock and, therefore, apart from the noise, the equity price (or return) is governed only by its fundamental value. Second, our approach will facilitate to segregate the short-run expectation of the equity return from the long-run expectation. The short run expectation of the return of the equity depends, with other factors, on market sentiments. However, in the long run, the market reaches its normal position where effects of sentiments are zero and, therefore, the expectation would be consistent with the fundamentals. In this connection, our empirical study for Indian equity market has established the following: original equity market returns are autocorrelated for at least one lag, however the hypothetical market returns are, in general, not so autocorrelated. Therefore, transformed returns comprising the hypothetical market meet the prerequisites of applying an asset-pricing model and, therefore, any conventional bond or stock pricing model could be efficiently manipulated for those returns. The approach will widen the scope of asset-pricing models ranging from a strict efficient market to an inefficient market. @Debasish Majumder is Assistant Adviser (email) in the Department of Statistics and Information Management, Reserve Bank of India. *The views expressed in this paper are those of the author alone and not of the institution to which he belongs. 1Majumder (2006) developed his model for stock pricing in the context of modeling credit risk. 2Details of these indices are available in the NSE-India site: www.nse-india.com. Daily portfolio price data are obtained from the above site. 3This quote is drawn from Finkelstein (2006) References Andersen, T., T. Bollerslev, F. Diebold, and P. Labys (2003), Modeling and Forecasting Realized Volatility, Econometrica 71: 579-625. Avramov, D., T. Chordia, and M. Goyal (2006), Liquidity and Autocorrelations in Individual Stock Returns, The Journal of Finance 61: 2365-2394. Barberis, N., A. Shleifer, and R. Vishny (1998), A model of investor sentiment, Journal of Financial Economics 49: 307-343. BCBS, Bank for International Settlements (2009), Principles for sound stress testing practices and supervision, www.bis.org/publ/bcbs155.pdf. Bird, R., G. Menzies, P. Dixon, and M. Rimmer (2010), The economic costs of US stock mispricing, Journal of Policy Modeling, doi:10.1016/j.jpolmod.2010.10.010 Black, F., and M. Scholes (1973), The pricing of options and corporate liabilities, Journal of Political Economy 81: 637-659. Blandon, J.G. (2007), Return Auto correlation Anomalies in two European Stock Markets, Revista de Análisis Económico 22: 59-70. Blaschke Winfrid [et al.] Stress Testing of Financial Systems: An Overview of Issues, Methodologies, and FSAP Experiences [Online] // International Monetary Fund. - June 2001. - http://www.imf.org/external/pubs/ft/wp/2001/wp0188.pdf. Cutler, D., J. Poterba, and L. Summers (1989), What moves stock prices?, Journal of Portfolio Management 15: 4–12. Campbell, J. (1993), Intertemporal Asset Pricing Without Consumption Data, American Economic Review 83: 487-512. Chan, K. (1993), Imperfect information and cross-autocorrelation among stock prices, Journal of Finance 48: 1211 –1130. Chan, K.C., B.E. Gup, and Ming-Shiun. Pan (1997), International Stock Market Efficiency and Integration: A Study of Eighteen Nations, Journal of Business Finance & Accounting 24: 803–813. Chang, E.J., E.J.A. Lima, and B.M. Tabak (2004), Testing for predictability in emerging equity markets, Emerging Markets Review 5: 295-316. Chen, C.R., Y. Su, and Y. Huang (2008), Hourly index return autocorrelation and conditional volatility in an EAR–GJR-GARCH model with generalized error distribution, Journal of Empirical Finance 15: 789–798. Chopra, N., J. Lakonishok, and J.R. Ritter (1992), Measuring Abnormal Performance: Do Stocks Overreact?, Journal of Financial Economics 31: 235-268. Conrad, J., and G. Kaul (1988), Time-Variation in Expected Return, The Journal of Business 61: 409-425. Fama, E.F. (1970), Efficient Capital Markets: A Review of Theory and Empirical Work, Journal of Finance 25: 383-417. Fama, E.F. (1991), Efficient Capital Markets: II, Journal of Finance 46: 1575-1617. Fama, E.F. (1998), Market efficiency, long-term returns, and behavioral finance, Journal of Financial Economics 49: 283-306. Fama, E.F., and K.R. French (1988), Permanent and temporary components of stock market prices, Journal of Political Economy 96: 246-273. Finkelstein, B. (2006). The Politics of Public Fund Investing: How to Modify Wall Street to Fit Main Street. New York: Touchstone Publisher. Gregoriou, A., J. Hunter and F. Wu (2009), An empirical investigation of the relationship between the real economy and stock returns for the United States, Journal of Policy Modeling 31: 133–143. Guo, H., and R. Savickas (2006), Understanding Stock Return Predictability, Working Paper 2006-019B, Federal Reserve Bank of St. Louis. Harvey, C.R. (1995a), Predictable risk and returns in emerging markets, The Review of Financial Studies 8: 773-816. Harvey, C.R. (1995b), The Risk Exposure of Emerging Equity Markets, World Bank Economic Review 9: 19-50. Jegadeesh, N. (1990), Evidence of Predictable Behavior of Security Returns, The Journal of Finance 45: 881-898. Jegadeesh, N., and S. Titman (1993), Returns to buying winners and selling losers: implications for stock market efficiency, Journal of Finance 48: 65-91. Knif, J., S. Pynnonen, and M. Luoma (1996), Testing for common autocorrelation features of two Scandinavian stock markets, International Review of Financial Analysis 5: 55– 64. Koutmos, G. (1997), Do emerging and developed stock markets behave alike? Evidence from six Pacific Basin stock markets, Journal of International Financial Markets, Institutions and Money 7: 221–234. Kramer, W. (1998), Note: Short-term predictability of German stock returns, Empirical Economics 23: 635-639. LeBaron, B. (1992), Some relations between volatility and serial correlations in stock market returns, Journal of Business 65: 199–219. Leroy, S., and R. Porter (1981), The Present Value Relation: Test Based on Variance Bounds, Econometrica 49: 555-577. Lintner, J. (1965), The valuation of risk assets on the selection of risky investments in stock portfolios and capital budgets, Review of Economics and Statistics 47: 13-37. Lo, Andrew.W., and A.C. MacKinlay (1988), Stock market prices do not follow random walks: Evidence from a simple specification test, Review of Financial Studies 1: 41-66. Majumder, D. (2006), Inefficient markets and credit risk modeling: Why Merton’s model failed, Journal of Policy Modeling 28: 307-318. Malkiel, B.G. (2003), The Efficient Market Hypothesis and Its Critics, Journal of Economic Perspectives 17: 59–82. Malkiel, B.G. (2005), Reflections on the Efficient Market Hypothesis: 30 Years Later, The Financial Review 40: 1–9. McKenzie, M.D., and R.W. Faff (2005), Modeling conditional return autocorrelation, International Review of Financial Analysis 14: 23– 42. Merton, R.C. (1973), An intertemporal capital asset pricing model, Econometrica 41: 867-887. Merton, R. (1980), On Estimating the Expected Return on the Market: An Exploratory Investigation, Journal of Financial Economics 8: 323-361. Mollah, A.S. (2007), Testing weak-form market efficiency in emerging market: evidence from Botswana stock exchange, International Journal of Theoretical and Applied Finance 10: 1077-1094. Parametric Portfolio Associates (2008), Emerging Markets: Portfolio structuring to capture long term growth, Emerging Markets Whitepaper, spring, http://www.parametricportfolio.com/. Pesaran, M.H., and A. Timmermann (1995), Predictability of Stock Returns: Robustness and Economic Significance, The Journal of Finance 50: 1201-1228. Poterba, J., and L. Summers (1988), Mean Reversion in Stock Prices: Evidence and Implications, Journal of Financial Economics 22: 27-59. Ross, S. (1976), The arbitrage theory of capital asset pricing, Journal of Economic Theory 13: 341–60. Rubinstein, M. (2001), Rational markets: Yes or no? The affirmative case, Financial Analysts Journal 57: 15–28. Sharpe, W.F. (1964), Capital asset prices: A theory of market equilibrium under conditions of risk, Journal of Finance 19: 425-442. Shiller, R.J. (1981), Do Stock Prices Move Too Much To Be Justified by Subsequent Changes in dividends?, American Economic Review 71: 421-436. Shiller, R.J. (1987), Fashions, Fads and Bubbles in Financial Markets, in: Knights, Raiders and Targets, eds., The Impact of the Hostile Takeover, Oxford University Press, UK. Appendix: Modeling predictable component of the of the market return
On account of monitoring the performance of the overall economy or a sector of the economy National Stock Exchange (NSE), India maintains 11 major indices and 14 sectoral indices:
These indices are computed on a free float-adjusted market capitalization weighted methodology and are used extensively in empirical research. Historical data for daily closing prices for these indices is available in the NSE-India site. From this list of indices, we have chosen 6 portfolios for our analysis. These portfolios are: S&P CNX Nifty (P1), CNX Nifty Junior (P2), S&P CNX Defty (P3), Bank Nifty (P4), CNX Midcap (P5) and CNX Infrastructure (P6). Data on daily closing prices for these 6 indices for the period January, 2003 to March, 2009 has been downloaded from the above site. |
ପେଜ୍ ଅନ୍ତିମ ଅପଡେଟ୍ ହୋଇଛି: